Geometry kite shape

Properties of a kite are the distinct characteristics or features of the kite shape, its vertices, geometry kite shape, interior angles, sides, diagonals that makes it a unique shape. A kite is a quadrilateral, a closed flat geometric shape in which two sets of neighboring or adjacent sides are congruent equal in length. Its diagonals meet at right angles.

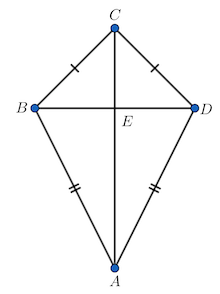
A kite shape is a quadrilateral that has 2 pairs of equal adjacent sides. Let us learn more about the properties of a kite shape. A kite shape is a quadrilateral in which two pairs of adjacent sides are of equal length. No pair of sides in a kite are parallel but one pair of opposite angles are equal. A kite is a quadrilateral that has two pairs of consecutive equal sides and perpendicular diagonals. The longer diagonal of a kite bisects the shorter one. Observe the following kite ACBD to relate to its properties given below.

Geometry kite shape

In Euclidean geometry , a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite to each other instead of being adjacent. Kite quadrilaterals are named for the wind-blown, flying kites , which often have this shape and which are in turn named for a bird. Kites are also known as deltoids , but the word "deltoid" may also refer to a deltoid curve, an unrelated geometric object. A kite, as defined above, may be either convex or concave, but the word "kite" is often restricted to the convex variety. A concave kite is sometimes called a "dart" or "arrowhead", and is a type of pseudotriangle. It is possible to classify quadrilaterals either hierarchically in which some classes of quadrilaterals are subsets of other classes or as a partition in which each quadrilateral belongs to only one class. With a hierarchical classification, a rhombus a quadrilateral with four sides of the same length or a square is considered to be a special case of a kite, because it is possible to partition its edges into two adjacent pairs of equal length. According to this classification, every equilateral kite is a rhombus, and every equiangular kite is a square. However, with a partitioning classification, rhombi and squares are not considered to be kites, and it is not possible for a kite to be equilateral or equiangular. For the same reason, with a partitioning classification, shapes meeting the additional constraints of other classes of quadrilaterals, such as the right kites discussed below, would not be considered to be kites. The remainder of this article follows a hierarchical classification, in which rhombi, squares, and right kites are all considered to be kites. By avoiding the need to treat special cases differently, this hierarchical classification can help simplify the statement of theorems about kites. The kites that are also cyclic quadrilaterals i.

Classified hierarchically, kites include the rhombi quadrilaterals with four equal sides and squares. A dart or an arrowhead is an example of a concave kite.

In Euclidean geometry , a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids , [1] but the word deltoid may also refer to a deltoid curve , an unrelated geometric object sometimes studied in connection with quadrilaterals. Every kite is an orthodiagonal quadrilateral its diagonals are at right angles and, when convex, a tangential quadrilateral its sides are tangent to an inscribed circle. The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites , with two opposite right angles; the rhombi , with two diagonal axes of symmetry; and the squares , which are also special cases of both right kites and rhombi. Kites of two shapes one convex and one non-convex form the prototiles of one of the forms of the Penrose tiling.

You probably know a kite as that wonderful toy that flies aloft on the wind, tethered to you by string. That toy kite is based on the geometric shape, the kite. A kite is a quadrilateral shape with two pairs of adjacent touching , congruent equal-length sides. That means a kite is all of this:. Sometimes a kite can be a rhombus four congruent sides , a dart, or even a square four congruent sides and four congruent interior angles. Some kites are rhombi, darts, and squares. Not every rhombus or square is a kite.

Geometry kite shape

A kite shape is a quadrilateral that has 2 pairs of equal adjacent sides. Let us learn more about the properties of a kite shape. A kite shape is a quadrilateral in which two pairs of adjacent sides are of equal length. No pair of sides in a kite are parallel but one pair of opposite angles are equal.

Oakwood mall eau claire movies

Its diagonals meet at right angles. A quadrilateral is a kite if and only if any one of the following conditions is true:. Sandaruwan Fonseka. But what would happen if these two diagonals are both perpendicular bisectors of each other? So one definition that you could make for a kite is that you have two pairs of congruent sides, where the congruent sides are adjacent. And then I'm going to make another segment, but they're going to be perpendicular bisectors of each other. If the congruent sides aren't adjacent, what else could they be? Are Rhombi and squares also called kites? Saudi Arabia. As the above Tristan said , it has to go from the middle of a certain line which means divides into two equal parts and also it has to make a 90 degree angle by both lines. Then you have a subset of-- I guess I could say-- rhombi, and you get to a square. And they are adjacent.

In Euclidean geometry , a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides.

Because they circumscribe one circle and are inscribed in another circle, they are bicentric quadrilaterals. Correct Incorrect. For the same reason, with a partitioning classification, shapes meeting the additional constraints of other classes of quadrilaterals, such as the right kites discussed below, would not be considered to be kites. Kite geometry facts for kids Kids Encyclopedia Facts. Posted 9 years ago. The other thing we know about kites is that one of these lines is bisecting the other of the two. You could start with a line, and then you could construct a perpendicular bisector of that line, another segment that bisects it at a degree angle. No, a kite is not a parallelogram. Is a kite a parallelogram? Correct answer is: perpendicular Diagonals of a kite are perpendicular. Learn Properties Of Kite with tutors mapped to your child's learning needs. So let's make that a constraint. Read Edit View history. Suggest an edit.