Derivative ln x
In this lesson, we are going to see what is the derivative of ln x.
Part of calculus is memorizing the basic derivative rules like the product rule, the power rule, or the chain rule. One of the rules you will see come up often is the rule for the derivative of lnx. In the following lesson, we will look at some examples of how to apply this rule to finding different types of derivatives. We will also see how using the laws of logarithms can help make taking these kinds of derivatives even easier. This allows us to find the following. These show you the more straightforward types of derivatives you can find using this rule. But, if we combine this with the laws of logarithms we can do even more.
Derivative ln x
.
Multiplication Tables.
.
Now that we have the derivative of the natural exponential function, we can use implicit differentiation to find the derivative of its inverse, the natural logarithmic function. Differentiating both sides of this equation results in the equation. We may also derive this result by applying the inverse function theorem, as follows. Figure 3. At first glance, taking this derivative appears rather complicated. However, by using the properties of logarithms prior to finding the derivative, we can make the problem much simpler. Using the derivative above, we see that. Try It.
Derivative ln x
This guide will show you the derivative of ln x and how to use this rule to help you solve even more complex derivatives! Of course, we assume or recommend that you understand the basic concepts of a derivative first. The formula to finding the derivative of a natural log is actually quite simple:.
Kbb camper
Instead, here, you MUST use the chain rule. No, the derivative of ln x is NOT the same as the derivative of log x. Privacy Policy. In the example above, only one rule was needed to fully expand the expression. Before applying any calculus rules, first expand the expression using the laws of logarithms. Learn Derivative Of Ln X with tutors mapped to your child's learning needs. Example 3: Find the derivative of x ln x. But the fact is that their derivatives are NOT equal. But, if we combine this with the laws of logarithms we can do even more. For detailed proof, click on the following:. Since the exponent is only on the x, we will need to first break this up as a product, using rule 2 above.
In this lesson, we are going to see what is the derivative of ln x.
This is the calculus step. Let us observe the first few derivatives of ln x in order to derive its n th derivative:. This step is all algebra; no calculus is done until after we expand the expression. The natural logarithm is denoted by "ln". Each of the derivatives above could also have been found using the chain rule. Maths Questions. Terms and Conditions. Example 2: Find the derivative of ln x 2. However, there are some cases where you have no choice. Before applying any calculus rules, first expand the expression using the laws of logarithms. One of the rules you will see come up often is the rule for the derivative of lnx. In the example above, only one rule was needed to fully expand the expression. About Us. Since the exponent is only on the x, we will need to first break this up as a product, using rule 2 above. Examples on Derivative of ln x Example 1: Find the derivative of ln 2x - 3.

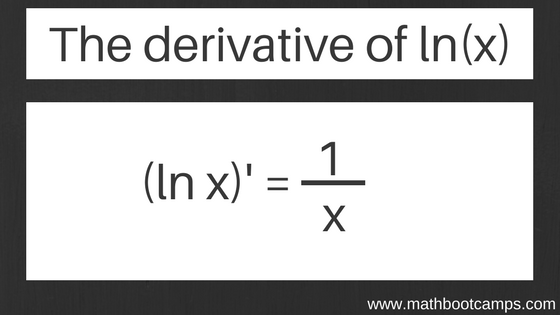
It is interesting. Tell to me, please - where to me to learn more about it?