X 2 8x 16
This site is best viewed with Javascript.
Solve Practice Play. Game Central. Greatest Common Factor. Least Common Multiple. Order of Operations.
X 2 8x 16
.
Other Ways to Solve Quadratic equations. Solve for a Variable.
.
Solve Practice Play. Game Central. Greatest Common Factor. Least Common Multiple. Order of Operations. Mixed Fractions. Prime Factorization. Solve for a Variable.
X 2 8x 16
Please ensure that your password is at least 8 characters and contains each of the following:. Enter a problem Algebra Examples Popular Problems. Find the x-intercepts.
Stainless steel dish drainer rack
Greatest Common Factor. Algebra Calculator. Least Common Multiple. The trinomial square is the square of the binomial that is the sum or difference of the square roots of the leading and trailing terms, with the sign determined by the sign of the middle term of the trinomial square. List all such integer pairs that give product Conclusion : Trinomial can not be factored. Mixed Fractions. Latest Related Drills Solved. Trinomial squares can be factored by finding the square roots of the leading and trailing terms. Steps Using Square Of Binomial. To find a and b, set up a system to be solved. Rewrite as a binomial square. Substitute the value of u to compute the r and s. Express r and s with respect to variable u.
.
Game Central. The values of r and s are equidistant from the center by an unknown quantity u. That is, if the parabola has indeed two real solutions. Since ab is positive, a and b have the same sign. Trinomial squares can be factored by finding the square roots of the leading and trailing terms. Linear Equations. Order of Operations. Factor the expression by grouping. The trinomial square is the square of the binomial that is the sum or difference of the square roots of the leading and trailing terms, with the sign determined by the sign of the middle term of the trinomial square. Our parabola opens up and accordingly has a lowest point AKA absolute minimum.

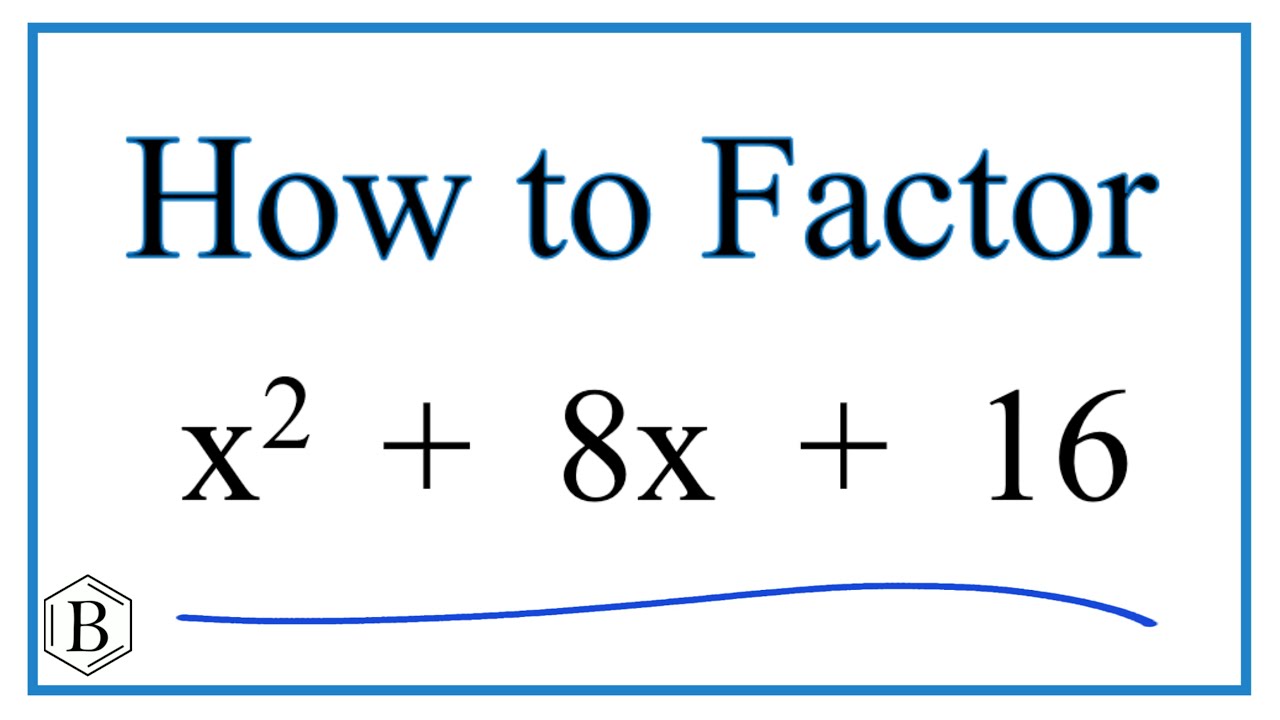
I can recommend to visit to you a site on which there are many articles on a theme interesting you.
It is removed (has mixed section)
I can not participate now in discussion - it is very occupied. But I will return - I will necessarily write that I think on this question.