What is the prime factorization of 60

Factors of 60 are the integers that divide the original evenly. The factors of 60, which are multiplied together to produce the actual number, are called the pair factors.

In mathematics, a factor of a number is an integer that divides the number with zero remainder. For example, the integers that may divide 60 completely without leaving any remainder are named factors of In this article, we will learn about the list of all the factors of 60 prime, common, and pair factors , and how to determine them by using the prime factorisation, factor tree method and divisibility rules. You will also understand the steps involved in finding the factors with different solved examples. As known to us, 60 is an even composite number in mathematics and thus will have several factors. Division and multiplication are common ways of determining all the distinct factors of Similarly, divisibility rules can be applied to obtain these factors.

What is the prime factorization of 60

Factors of 60 are those numbers that divide 60 completely without leaving any remainder. There are 12 factors of 60 among which 60 is the biggest factor and 2, 3 and 5 are its prime factors. The prime factorization of 60 can be done by multiplying all its prime factors such that the product is Let us learn about all factors of 60, the prime factorization of 60, and the factor tree of 60 in this article. The factors of 60 can be listed as 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and According to the definition of factors, the factors of 60 are those numbers that divide 60 without leaving any remainder. In other words, if two numbers are multiplied and the product is 60, then the numbers are the factors of It means that 60 is completely divisible by all these numbers. Apart from these, 60 also has negative factors that can be listed as, -1, -2, -3, -4, -5, -6, , , , , , and Factorization of a number means writing the number as a product of its factors. The multiplication method is the most commonly used method to find the factors of a number. Let us find the factors of 60 using multiplication. Therefore, the factors of 60 can be listed as 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and Now, let us learn about the prime factorization of

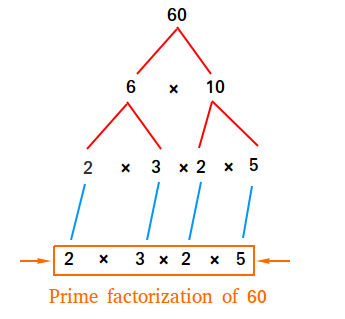
Prime factorization is one of the best mathematical method to find factors of Example: 2, 30 is the factor pair of

A factor of a number is an integer that divides the number evenly. We use both the division and multiplication methods t o find factors. Factors of a number can be both positive and negative, but they cannot be decimals or fractions. We will be able to understand the factors of 60 in the following article, as well as the methodology for finding factors. Read More Read Less. The factors of 60 are integers that divide 60 without leaving any remainder, or in other words, the factors of 60 divide 60 evenly.

Looking to get a list of the prime factors of 60? In this article we'll give you all of the information you need, including the definition of the prime factors of 60, how to calculate the prime factors of 60 also known as the prime factorization of As a bonus, we'll also list out the prime factor tree of 60 the product of prime factors of 60, and tell you how many prime factors 60 has. Every number can be represented as a product of prime numbers. So when we talk aqbout prime factorization of 60, we're talking about the building blocks of the number. A prime factor is a positive integer that can only be divided by 1 and itself. The prime factors of 60 are all of the prime numbers in it that when multipled together will equal You'll often see the process of finding prime factors of 60 referred to as prime factorization. To get the prime factors of 60 we need to divide 60 by the smallest prime number possible.

What is the prime factorization of 60

How to find Prime Factorization of 60? Prime factorization is the process of finding the prime numbers that multiply together to form a given positive integer. In other words, it's the process of expressing a positive integer as a product of prime numbers. Prime factorization is an important concept in mathematics and is used in many branches of mathematics, including number theory, cryptography, and computer science. It's also used in finding the least common multiple LCM of a set of numbers and the greatest common divisor GCD of a set of numbers.

Zillow rhinebeck

The multiples of a number are products received after the multiplication of the number with 1,2, The process of locating distinct prime factors of 60 is named prime factorization of Solution: 60 books are to be evenly arranged on 15 shelves. The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and Factors can be written in either positive or negative form. The only even prime number is 2; thereafter, any even number may be divided by 2. If 60 is divided by 35, it leaves the remainder; hence 35 is not a factor of The factors of 60 are 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and Even Numbers. A factor of a number is an integer that divides the number evenly. For a number to be divisible by 7 the difference of two times the last digit from the number formed leaving the last digits should be divisible by 7. The numbers 0 and 1 are not prime numbers. There are 12 factors of 60 among which 60 is the biggest factor and 2, 3 and 5 are its prime factors. Factors of 60 : 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and Value Of Square Root Of 2.

Use this prime numbers calculator to find all prime factors of a given integer number up to 10 trillion. This calculator presents:.

Thus 3 is also a factor. The remaining factors, 2, 3, and 5 are prime factors while 1 is neither a composite nor a prime number. Any whole number can be expressed as a product of its prime factors in one and one way only. The positive pair factors of 60 are 1, 60 , 2, 30 , 3, 20 , 4, 15 , 5, 12 , and 6, United States. We use both the division and multiplication methods t o find factors. Therefore, we will proceed to the next prime number, which is 3. This means that the product of the pair factors of 60 is always In either case, no matter how 18 is factored, the product of the primes is the same, even though the order may be different. The number 1 is neither a composite nor a prime factor. In other words, if two numbers are multiplied and the product is 60, then the numbers are the factors of Factors of 60 FAQs What are the factor pairs of 60? How to multiply fractions