Slope of a line passing through two points

The equation of a line is an algebraic method to represent a set of points that together form a line in slope of a line passing through two points coordinate system. The various points that together form a line in the coordinate axis can be represented as a set of variables x, y in order to form jellyfin clients algebraic equation, also referred to as the equation of a line. By dbza the equation of a line, it is possible to find whether a given point lies on the line. The equation of any line is a linear equation having a degree of one.

There are different formulas to find the slope with different types of available information about the line. Finding the slope from two points formula is specifically used when two points on the line are given. Let us see how to derive the formula for finding the slope from two points and also we will solve a few examples using the formula. We can use the same formula to derive the above formula also. Hence, we derived the slope formula. We can visualize this in the figure below.

Slope of a line passing through two points

Slope, sometimes referred to as gradient in mathematics, is a number that measures the steepness and direction of a line, or a section of a line connecting two points, and is usually denoted by m. Generally, a line's steepness is measured by the absolute value of its slope, m. The larger the value is, the steeper the line. Given m , it is possible to determine the direction of the line that m describes based on its sign and value:. Slope is essentially the change in height over the change in horizontal distance, and is often referred to as "rise over run. In the case of a road, the "rise" is the change in altitude, while the "run" is the difference in distance between two fixed points, as long as the distance for the measurement is not large enough that the earth's curvature should be considered as a factor. The slope is represented mathematically as:. The above equation is the Pythagorean theorem at its root, where the hypotenuse d has already been solved for, and the other two sides of the triangle are determined by subtracting the two x and y values given by two points. Given the points 3,4 and 6,8 find the slope of the line, the distance between the two points, and the angle of incline:. While this is beyond the scope of this calculator, aside from its basic linear use, the concept of a slope is important in differential calculus. For non-linear functions, the rate of change of a curve varies, and the derivative of a function at a given point is the rate of change of the function, represented by the slope of the line tangent to the curve at that point. Financial Fitness and Health Math Other. By definition, the slope or gradient of a line describes its steepness, incline, or grade.

But the magic doesn't stop there, for you also get a bunch of extra results for good measure: The equation of your function same as the equation of the line. Because of this fact, it is said that the slope of this vertical line is undefined. Maths Program.

The slope calculator determines the slope or gradient between two points in the Cartesian coordinate system. The slope is basically the amount of slant a line has and can have a positive, negative, zero, or undefined value. Before using the calculator, it is probably worth learning how to find the slope using the slope formula. To find the equation of a line for any given two points that this line passes through, use our slope intercept form calculator. Here, we will walk you through how to use this calculator, along with an example calculation, to make it simpler for you. To calculate the slope of a line, you need to know any two points on it:.

The slope calculator determines the slope or gradient between two points in the Cartesian coordinate system. The slope is basically the amount of slant a line has and can have a positive, negative, zero, or undefined value. Before using the calculator, it is probably worth learning how to find the slope using the slope formula. To find the equation of a line for any given two points that this line passes through, use our slope intercept form calculator. Here, we will walk you through how to use this calculator, along with an example calculation, to make it simpler for you.

Slope of a line passing through two points

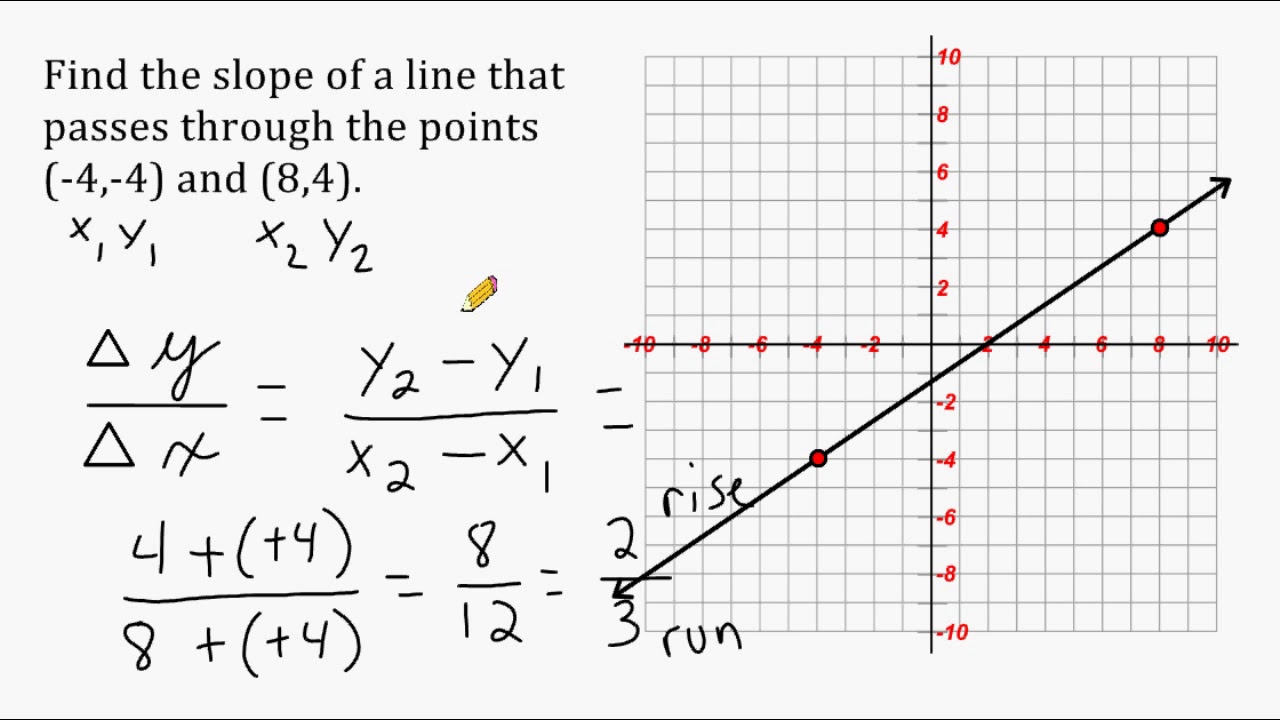
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Learn how to write the slope formula from scratch and how to apply it to find the slope of a line from two points.

Law and order svu stabler

Consider two points on a line—Point 1 and Point 2. Kindergarten Worksheets. You can use this calculator in reverse and find a missing x or y coordinate! This number is the gradient of the hill if it increases linearly. Sometimes we need to find the slope of a line between two points and we might not have a graph to count out the rise and the run. Say you know two points on a line and their coordinates are 2, 5 and 9, Make sure that the points you measure from are the same as step 1. Input two points using numbers, fractions, mixed numbers or decimals. The coefficient of x will be the slope. Using the Slope Formula to Find the Slope between Two Points Learning Outcomes Use the slope formula to find the slope of a line between two points Find the slope of horizontal and vertical lines. If it does not, repeat the steps but at where there is a noticeable change in slope. How do you calculate the slope of a hill? There are different formulas to find the slope with different types of available information about the line. Y - intercept.

The slope of a line is its vertical change divided by its horizontal change, also known as rise over run.

Make sure that the points you measure from are the same as step 1. By using the equation of a line, it is possible to find whether a given point lies on the line. This can be found by first calculating the slope, by dividing the change in the y direction by the change in the x direction, and then finding the inverse tangent of the slope. Add the two values together. Input two points using numbers, fractions, mixed numbers or decimals. Apart from the method that is already shown above, we can derive the formula of finding slope from two points in different methods. You can just use the coordinates, keeping careful track of which is Point 1 and which is Point 2. To find the slope of a line, we need two coordinates on the line. Input the values into the formula. Maths Questions. Our Mission. Example Advanced What is the slope of the line that contains the points [latex] 3, Learn Practice Download.