Root mean square speed
Other sections state that increasing the temperature increases the speeds at which molecules move. We are now in a position to find just how large that increase is for a gaseous substance. Combining the ideal gas law with Eq.
We have examined pressure and temperature based on their macroscopic definitions. Pressure is the force divided by the area on which the force is exerted, and temperature is measured with a thermometer. We can gain a better understanding of pressure and temperature from the kinetic theory of gases , the theory that relates the macroscopic properties of gases to the motion of the molecules they consist of. First, we make two assumptions about molecules in an ideal gas. To derive the ideal gas law and the connection between microscopic quantities such as the energy of a typical molecule and macroscopic quantities such as temperature, we analyze a sample of an ideal gas in a rigid container, about which we make two further assumptions:. The collisions between molecules do not appear in the derivation of the ideal gas law. They do not disturb the derivation either, since collisions between molecules moving with random velocities give new random velocities.
Root mean square speed
Determine the most probable, average and root-mean-square speed of gas molecules described by the Maxwell-Boltzmann distribution. Maxwell-Boltzmann distribution describes a classical system of distinguishable particles, such as for example molecules. A distribution function for the magnitude of velocity of the molecules is defined as follows. The most probable speed of gas molecules described by the Maxwell-Boltzmann distribution is the speed at which distribution graph reaches its maximum. Thus, if we know the formula of this distribution, we just need to differentiate it and consider the derivative to be equal to zero. Speed for which the derivate equals zero is the most probable speed. The average speed of molecules is the mean of all magnitudes of velocity at which molecules of the given gas are moving. The root-mean-square speed of molecules is the speed at which all the molecules have the same total kinetic energy as in case of their actual speed. The average speed of molecules can be calculated as an integral of the Maxwell-Boltzmann distribution function multiplied by the magnitude of velocity of a molecule v. The variable of integration, velocity, can attain all possible values, therefore we integrate from zero to infinity. The root-mean-square speed can be calculated in a similar way, the only difference is that we multiply the Maxwell-Boltzmann distribution function by v 2.
Then we make use of the fact that neither the factored-out constants nor the value of the exponential function can be equal to zero.
Gases are made up of individual atoms or molecules freely moving in random directions with a wide variety of speeds. Kinetic molecular theory tries to explain the properties of gases by investigating the behavior of individual atoms or molecules making up the gas. This example problem shows how to find the average or root mean square velocity rms of particles in a gas sample for a given temperature. Solution: Root mean square velocity is the average velocity of the molecules that make up a gas. Use the gas constant 8. The units on R use kg, so the molar mass must also use kg.
Root mean square speed v rms. Root mean square speed v rms is defined as the square root of the mean of the square of speeds of all molecules. Equation 9. From the equation 9. At a given temperature the molecules of lighter mass move faster on an average than the molecules with heavier masses. We can also write the v rms in terms of gas constant R. Where N A is Avogadro number. The root mean square speed or r. The equation 9.
Root mean square speed
For alternating electric current , RMS is equal to the value of the constant direct current that would produce the same power dissipation in a resistive load. The RMS value of a set of values or a continuous-time waveform is the square root of the arithmetic mean of the squares of the values, or the square of the function that defines the continuous waveform. In physics, the RMS current value can also be defined as the "value of the direct current that dissipates the same power in a resistor. The RMS value of a continuous function or signal can be approximated by taking the RMS of a sample consisting of equally spaced observations. Additionally, the RMS value of various waveforms can also be determined without calculus , as shown by Cartwright. In the case of the RMS statistic of a random process , the expected value is used instead of the mean. If the waveform is a pure sine wave , the relationships between amplitudes peak-to-peak, peak and RMS are fixed and known, as they are for any continuous periodic wave.
Wheeljack
Remarkably, Bernoulli did this work before Dalton established the view of matter as consisting of atoms. In a sample of gas in a container, the randomness of the molecular motion causes the number of collisions of molecules with any part of the wall in a given time to fluctuate. Graham's Formula of Diffusion and Effusion. Electrical engineers often need to know the power , P , dissipated by an electrical resistance , R. You may accept or manage your choices by clicking below, including your right to object where legitimate interest is used, or at any time in the privacy policy page. We now use the definition of the average, which we denote with a bar, to find the force:. We make still further assumptions that simplify the calculations but do not affect the result. Sign in. Identify the knowns and unknowns and determine which equations to use to solve the problem. Second, we begin by considering monatomic gases, those whose molecules consist of single atoms, such as helium. As we have seen from kinetic theory, when the gases have the same temperature, their molecules have the same average kinetic energy. First, we let the container be a rectangular box.
Other sections state that increasing the temperature increases the speeds at which molecules move. We are now in a position to find just how large that increase is for a gaseous substance. Combining the ideal gas law with Eq.
Measure advertising performance. Sign in. Use profiles to select personalised advertising. Archived from the original on In a sample of gas in a container, the randomness of the molecular motion causes the number of collisions of molecules with any part of the wall in a given time to fluctuate. We have assumed that a molecule is small compared with the separation of molecules in the gas, and that its interaction with other molecules can be ignored. The magnitude of the most probable velocity of molecules of the gas described by Maxwell-Boltzmann distribution is given by the relation. We will return to this point when discussing diatomic and polyatomic gases in the next section. Archived from the original PDF on 15 January For a gas to be nearly ideal, as air is under ordinary conditions, the molecules must be very far apart. In the common case of alternating current when I t is a sinusoidal current, as is approximately true for mains power, the RMS value is easy to calculate from the continuous case equation above. The RMS speed of an ideal gas is calculated using the following equation:.

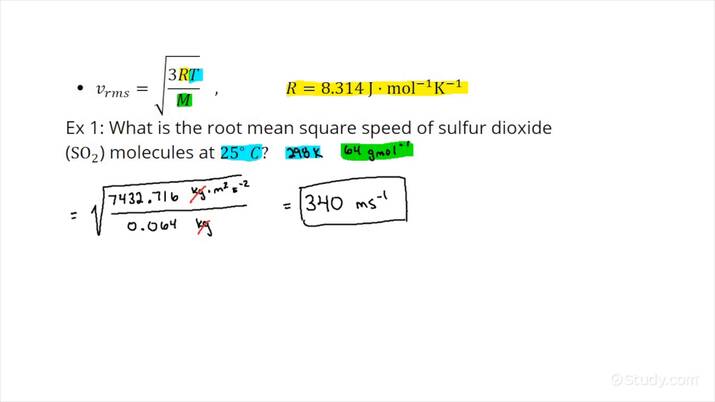
0 thoughts on “Root mean square speed”