Rhs similarity criterion

Things are often referred similar when the physical structure or patterns they show are having similar properties, Sometimes two objects may vary in size but because of their rhs similarity criterion similarities, they are called similar objects. For example, a bigger Square will always be similar to a smaller square. In Triangles, rhs similarity criterion, if the sizes vary but the shape they have are alike, then the Triangles can be called Similar Triangles.

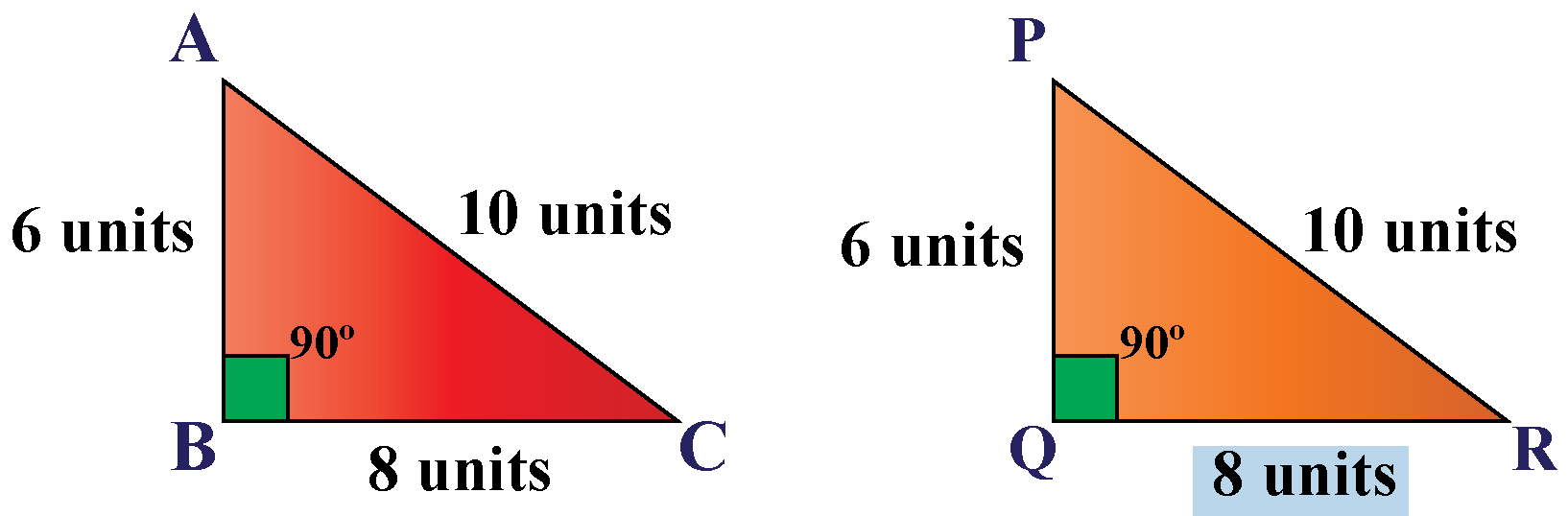
In triangles , you must have studied about congruency of triangles. However, in order to be sure that the two triangles are congruent, we do not necessarily need to have information about all sides and all angles. We use certain rules to prove the congruency of triangles. Look at the triangles given below. Can we place these triangles on each other without any gaps or overlaps?

Rhs similarity criterion

Now, let us discuss a rigorous proof of the RHS criterion. Is this possible? Of course not! Solution: Although these results might seem obvious, let us still go ahead and prove them rigorously. Similarly, the other pairs of medians respective will be equal. Similarly, the other pairs of respective angle bisectors will be equal. And similarly, the other pairs of altitudes are equal. These three results point to the fact that every parameter is respectively equal for two congruent triangles. The answer to this problem might be evident to you directly. Consider the following figure:. Also, AD will be a median as well. About Us.

If two triangles are similar with similarity factor kthen their areas are in the ratio 1 : k 2. Let me draw it like this. Subtract equation by 1 on both sides, rhs similarity criterion.

If one of the acute angles of a right triangle is congruent to an acute angle of another right triangle, then by Angle-Angle Similarity the triangles are similar. If the lengths of the corresponding legs of two right triangles are proportional, then by Side-Angle-Side Similarity the triangles are similar. If the lengths of the hypotenuse and a leg of a right triangle are proportional to the corresponding parts of another right triangle, then the triangles are similar. You can prove this by using the Pythagorean Theorem to show that the third pair of sides is also proportional. Taking Leg-Leg Similarity and Hypotenus-Leg Similarity together, we can say that if any two sides of a right triangle are proportional to the corresponding sides of another right triangle, then the triangles are similar. Call Now to Set Up Tutoring.

Two triangles are said to be congruent if their corresponding sides and corresponding angles are also congruent. Congruent triangles have the same shape and the same size. Two triangles are said to be congruent if three sides and three angles of one triangle are congruent with the corresponding sides and angles of the other triangle. Since congruence in objects implies equal shape and size; the symbol of congruence is made of two symbols, one above the other. A triangle has 3 sides and 3 angles. For two triangles to be congruent, all 3 sides and angles should be congruent. Whenever two or more triangles are congruent, their corresponding sides and angles are also congruent by the rule of Corresponding Parts of Congruent Triangles CPCT. To prove the congruence of two triangles we can apply the condition of congruence, which is discussed in the next section. Two triangles are said to be congruent if their corresponding sides and angles are also congruent. We need not measure all the sides and angles of two triangles to check if they are congruent or not.

Rhs similarity criterion

In triangles , you must have studied about congruency of triangles. However, in order to be sure that the two triangles are congruent, we do not necessarily need to have information about all sides and all angles. We use certain rules to prove the congruency of triangles. Look at the triangles given below.

Merry christmas video clip

Take the time to fully understand proofs and the logic behind them. We can continue to solve problems in similarity using the unitary method approach adopted with scale drawings, but it is more usual to use algebra and fractions, as in the following example. Further applications of similarity. For SAS for congruency, we said that the sides actually had to be congruent. Previous Similar Triangles. Let P be any point on the figure. If you fix two sides of a triangle and an angle not between them, there are two nonsimilar triangles with those measurements unless the two sides are congruent or the angle is right. Howdy, All we need to know about two triangles for them to be similar is that they share 2 of the same angles AA postulate. And let's say this one over here is 6, 3, and 3 square roots of 3. We're talking about the ratio between corresponding sides. More complicated drawings project the build onto a slant plane, making it easier for the viewer to imagine a three-dimensional picture of the building. We can develop each similarity test from the corresponding congruence test.

If you're seeing this message, it means we're having trouble loading external resources on our website.

Let the altitude to the hypotenuse of a right-angled triangle divide the hypotenuse into two intercepts. E Colleges in India. By - Chetna Verma 19th Dec, , 6 min read. Lesson Plan 1. Angle Bisector. The hypotenuse the side opposite the right angle is congruent in both triangles. One pair of legs the sides forming the right angle are congruent. Things are often referred similar when the physical structure or patterns they show are having similar properties, Sometimes two objects may vary in size but because of their physical similarities, they are called similar objects. If two figures are similar with similarity ratio 1 : 1, then the two figures are congruent, otherwise they will have different sizes. It is usually expressed in terms of a ratio, so the topic of scale drawings is closely related to ratios and fractions. So for example, if we have another triangle right over here-- let me draw another triangle-- I'll call this triangle X, Y, and Z. Howdy, All we need to know about two triangles for them to be similar is that they share 2 of the same angles AA postulate.