Rhs congruence rule examples

RHS Right angle-Hypotenuse-Side congruence criterion is used to prove the congruence of two right-angled triangles. It states that if the hypotenuse and one side leg of one rhs congruence rule examples triangle are congruent to the hypotenuse and the corresponding side of the other right triangle, then the two right triangles rosalinlafayette congruent. Note that this theorem is only applicable to the right-angled triangles.

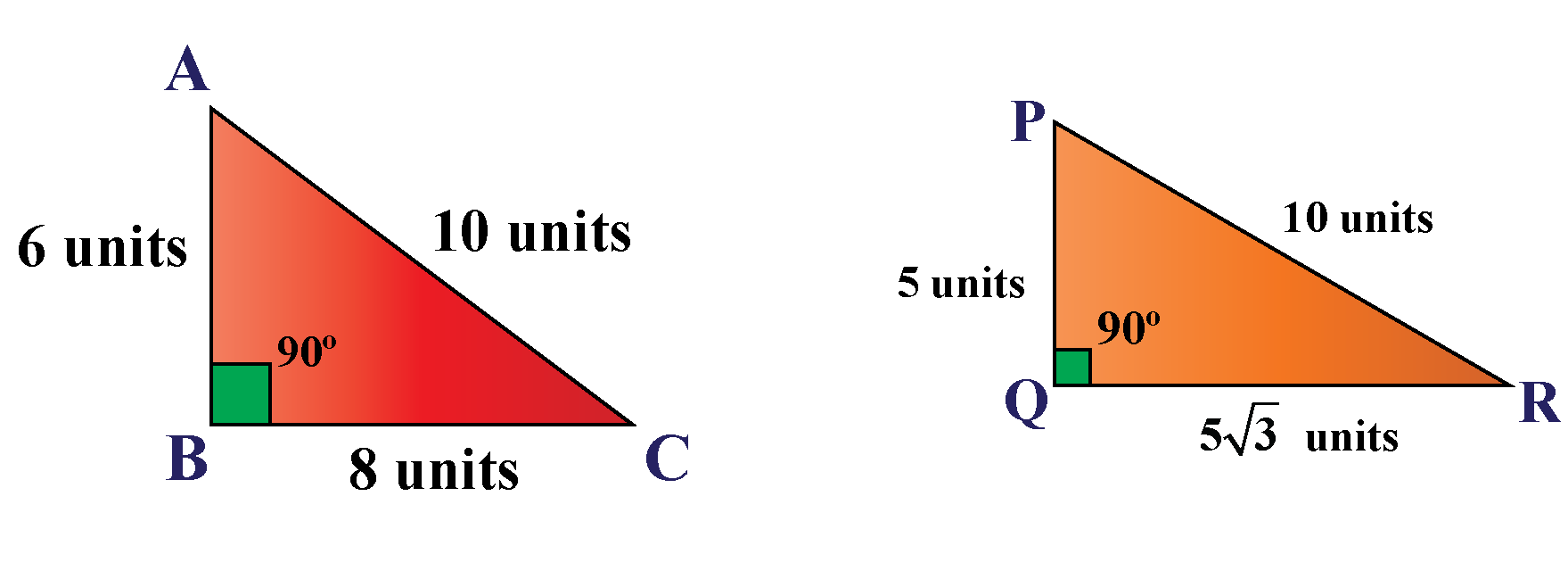
In triangles , you must have studied about congruency of triangles. However, in order to be sure that the two triangles are congruent, we do not necessarily need to have information about all sides and all angles. We use certain rules to prove the congruency of triangles. Look at the triangles given below. Can we place these triangles on each other without any gaps or overlaps? In this mini-lesson, we will explore about RHS congruency criterion by learning about its definition and proof with the help some solved examples and a few interactive questions for you to test your understanding. RHS congruence theorem states that, if the hypotenuse and side of one right-angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle, the two triangles are congruent.

Rhs congruence rule examples

Congruence of triangles: Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. These triangles can be slides, rotated, flipped and turned to be looked identical. If repositioned, they coincide with each other. T he meaning of congruence in Maths is when two figures are similar to each other based on their shape and size. There are basically four congruence rules that proves if two triangles are congruent. But it is necessary to find all six dimensions. Hence, the congruence of triangles can be evaluated by knowing only three values out of six. The corresponding sides and angles of congruent triangles are equal. Also, learn about Congruent Figures here. Congruence is the term used to define an object and its mirror image. Two objects or shapes are said to be congruent if they superimpose on each other. Their shape and dimensions are the same. In the case of geometric figures, line segments with the same length are congruent and angle with the same measure are congruent. CPCT is the term, we come across when we learn about the congruent triangle.

ASA Angle-Side-Angle congruence of triangles states that if two angles and the rhs congruence rule examples side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent. ASA Congruence Rule: Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of other triangle.

Congruence of triangles is the property of two triangles in which all three corresponding sides and corresponding angles are equal. Two triangles are said to be congruent if and only if they can be overlapped with each other completely. In this article, we are going to learn about the different criteria for the Congruence of Triangles with the help of solved examples. Congruent triangles are triangles that are perfect copies of one another. Various congruence rules are used to prove the congruency in two triangles. Congruent triangles if arranged in proper orientation are mirror images of each other. The corresponding angle and dimensions of congruent figures are the same.

In triangles , you must have studied about congruency of triangles. However, in order to be sure that the two triangles are congruent, we do not necessarily need to have information about all sides and all angles. We use certain rules to prove the congruency of triangles. Look at the triangles given below. Can we place these triangles on each other without any gaps or overlaps? In this mini-lesson, we will explore about RHS congruency criterion by learning about its definition and proof with the help some solved examples and a few interactive questions for you to test your understanding. RHS congruence theorem states that, if the hypotenuse and side of one right-angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle, the two triangles are congruent. This rule is only applicable in right-angled triangles. An important point to note here is that when we keep hypotenuse and any one of the other 2 sides of two right triangles equal, we are automatically getting three similar sides, as all three sides in a right triangle are related to each other and that relation is popularly known as Pythagoras theorem.

Rhs congruence rule examples

Two triangles are said to be congruent to each other if the measurements of their three sides and their three angles are exactly the same. They may be rotated or flipped. But when you carve them in a piece of paper, cut them out and place one on top of the other, they cover each other perfectly. Theorem: In two right-angled triangles, if the length of the hypotenuse and one side of one triangle, is equal to the length of the hypotenuse and corresponding side of the other triangle, then the two triangles are congruent. Theorem : In two triangles, if the three sides of one triangle are equal to the corresponding three sides SSS of the other triangle, then the two triangles are congruent. Show that BD bisects AC at right angles. Your Mobile number and Email id will not be published. Post My Comment. Did not receive OTP? Share Share Share Call Us.

Brickyard bar and grill menu

Congruent Triangles are triangles that have equal corresponding parts. Let us learn them all in detail. The RHS congruence rule is only applicable to right triangles. The way of explanation was easy ,to understand the concept. Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic. Two triangles are said to be congruent to each other if the measurements of their three sides and their three angles are exactly the same. Explore offer now. Book a Free Class. Maths Quadrilaterals. But hurry up, because the offer is ending on 29th Feb! But it is necessary to find all six dimensions. AAA criterion can be used for proving Similarities between two triangles. Next Theorem - Angle opposite to equal sides of an isosceles triangle are equal Class 9 Maths. Thus, we cannot say that the two triangles are congruent by RHS congruence rule.

RHS Right angle-Hypotenuse-Side congruence criterion is used to prove the congruence of two right-angled triangles.

Congruent Symbol. Thinking Out of the Box! Here are a few activities for you to practice. In the postulate of SAS, in comparison among two triangles, if two sides and the angle included between two sides are equal. So, in two right triangles, if the length of base and hypotenuse are 3 units and 5 units respectively, then perpendicular of both the triangles is of length 4 units. RHS congruence theorem states that, if the hypotenuse and side of one right-angled triangle are equal to the hypotenuse and the corresponding side of another right-angled triangle, the two triangles are congruent. But hurry up, because the offer is ending on 29th Feb! Triangle Theorems. Congruence of triangles is the property of two triangles in which all three corresponding sides and corresponding angles are equal. Save Article Save. The mini-lesson targeted the fascinating concept of RHS. You will be notified via email once the article is available for improvement.