Natural deduction solver
The Gateway to Logic is a collection of web-based logic programs offering a number of logical functions e. If you are a new user to the Gateway, consider starting with the natural deduction solver truth-table calculator or with the Server-side functions. On each category page, beneath the headline of the respective page, there are two important links: "Other programs" and "Help".
Mathematical logic is an area used throughout the engineering and scientific industries. Whether its developing artificial intelligence software or students completing a Computer Science degree, logic is a fundamental tool. In order to ensure that logic is used correctly a proof system must be used. Natural Deduction provides the tools needed to deduce and prove the validity of logical problems, making it a vital tool for everyone to learn to use. This is why many universities make it a priority to teach this to their students as they begin their studies.
Natural deduction solver
We have built an interactive proof checker that you can use to check your proofs as you are writing them. We can begin using it now, for simplification proofs. The checker needs to be initialized with a particular problem to solve. There isn't a simple interface that lets you create problems and feed them to the checker. But we have created a collection of them that you can work with. When it's time to do a proof, either as an example in one of our slides, or as part of a problem, you'll see the proof checker show up on your screen. You can create your proof with very little typing. You can cut an paste from previous lines or from the symbol list at the bottom of the proof area. To create a proof step, begin by choosing one or two statements from the list of available ones. Initially, there will just be premises. But, as you create new lines in the proof, they too will be available.
In some presentations of logic, different letters are used for propositional variables and arbitrary propositional formulas, but we will continue to blur the distinction.
Reflecting on the arguments in the previous chapter, we see that, intuitively speaking, some inferences are valid and some are not. The task of symbolic logic is to develop a precise mathematical theory that explains which inferences are valid and why. There are two general approaches to spelling out the notion of validity. In this chapter, we will consider the deductive approach: an inference is valid if it can be justified by fundamental rules of reasoning that reflect the meaning of the logical terms involved. We will now consider a formal deductive system that we can use to prove propositional formulas. There are a number of such systems on offer; the one will use is called natural deduction , designed by Gerhard Gentzen in the s.
This is an interactive solver for natural deduction proofs in propositional and first-order logic. The software focuses on digitizing the process of writing and evaluating natural deduction proofs while being easy to use and visually appealing in terms of resembling well handwritten proofs. These are a few of the main differences to other already existing proof solvers, as they are mostly addressed towards experienced logicians and need an extensive time to be properly understood and used. The purpose of this proof solver is to be an educational assistance for beginners and students in logic. Skip to content.
Natural deduction solver
NOTE: the program lets you drop the outermost parentheses on formulas with a binary main connective, e. Since the letter 'v' is used for disjunction, it can't be used as a variable or individual constant. Note also that quantifiers are enclosed by parentheses, e. NOTE: the order in which rule lines are cited is important for multi-line rules. Some importable sample proofs in the "plain" notation are here.
Minion sin fondo
This will be very helpful especially for students who are new to Natural Deduction proof techniques. Let us consider some more examples of natural deduction proofs. Source code The source is on github. If you think of them as propositional variables, just keep in mind that in any rule or proof, you can replace every variable by a different formula, and still have a valid rule or proof. Then we construct, separately, the following two proofs: Then we use these two proofs to construct the following one: Finally, we apply the implies-introduction rule to this proof to cancel the hypothesis and obtain the desired conclusion: The process is similar to what happens in an informal argument, where we start with some hypotheses, and work forward towards a conclusion. We can continue to cancel that hypothesis as well:. Natural Deduction for First Order Logic 9. At that point, we look to the hypotheses, and start working forward. For modal predicate logic, constant domains and rigid terms are assumed. You switched accounts on another tab or window. Reload to refresh your session. Correct answer is A. Examples click!
It also designates the type of reasoning that these logical systems embody.
R: It will rain. In order to remedy these problems I am building LogicAssistant which will have a number of useful features that will aid users with their Natural Deduction proofs. Any kind of feedback, problem report, or proposed improvement is welcome at any time. Correct answer is B. Click the "Export" button to export a completed proof. Any label will do, though we will tend to use numbers for that purpose. Accessibility is universal S5 reflexive symmetric transitive euclidean serial. There are obvious differences: we describe natural deduction proofs with symbols and two-dimensional diagrams, whereas our informal arguments are written with words and paragraphs. The motivation of LogicAssistant is to fill in these gaps left by existing solvers to help solve Natural Deduction proofs. Consider the sentence: He was not unaware that she was a student.

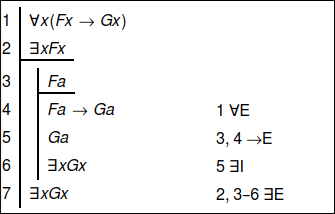
In my opinion you are not right. Write to me in PM, we will talk.
It is rather valuable information
In my opinion you are mistaken. I can prove it. Write to me in PM.