Limit x/sinx
This inequality is worth remembering, because it is useful not only for this proof, but for various other things in mathematical analysis for example, for estimating numerical series in a comparative convergence criterion, limit x/sinx. The limit x/sinx will look like this:. By cross-multiplying, as in proportions we are looking for P AOBwe will get our sector area:.
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Determining limits using the squeeze theorem. About About this video Transcript. We use a geometric construction involving a unit circle, triangles, and trigonometric functions. By comparing the areas of these triangles and applying the squeeze theorem, we demonstrate that the limit is indeed 1.
Limit x/sinx
.
These two cancel out. If I were to go all the way around the limit x/sinx, it would be two pi radians, so this is theta over to two pis of the entire circle and we know the area of the circle, limit x/sinx.
.
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. About About this video Transcript. Created by Sal Khan. Want to join the conversation? Log in. Sort by: Top Voted. Posted 12 years ago. Why do we consider x only in the first and the fourth quadrant?
Limit x/sinx
To use trigonometric functions, we first must understand how to measure the angles. The radian measure of an angle is defined as follows. We say the angle corresponding to the arc of length 1 has radian measure 1. Table shows the relationship between common degree and radian values. Trigonometric functions allow us to use angle measures, in radians or degrees, to find the coordinates of a point on any circle—not only on a unit circle—or to find an angle given a point on a circle. They also define the relationship among the sides and angles of a triangle. Definition: T rigonometric functions.
Pvz solar flare fanart
The numerator is bounded between 1 and -1, while the denominator goes to infinity, so the limit is 0. Arnav Sud. Same with the blue triangle being greater than or equal to the wedge. So the absolute values can be discarded. I mean, that proof made no sense in the beginning. The limit as theta approaches zero of this is going to be greater than or equal to the limit as theta approaches zero of this, which is the one that we care about, sine of theta over theta, which is going to be greater than or equal to the limit as theta approaches zero of this. Please tell me, I want to know, of some way to actually think of doing bizarre things like that to prove what we want. You can't just think of proofs like that out of thin air! Polish Ed. Your objection is well-placed, and you're correct that proof-writing is a skill that is mostly improved by practice. Math major here.
Wolfram Alpha computes both one-dimensional and multivariate limits with great ease. Determine the limiting values of various functions, and explore the visualizations of functions at their limit points with Wolfram Alpha.
Now let's think about the area of this wedge that I am highlighting in this yellow color. Remember, this is a unit circle. Log in. What would tangent of theta be? And once he had made the decision to compare areas, the proof was fairly straightforward algebra. Same with the blue triangle being greater than or equal to the wedge. Sine of theta over theta is defined over this interval, except where theta is equal to zero. Sine of theta over theta is defined over this interval, except where theta is equal to zero. Sal's primary target audience is U. I'll rewrite it over here. And if we wanted to make this work for thetas in the fourth quadrant, we could just write an absolute value sign right over there 'cause we're talking about positive area. And the reason why I did that is we can now divide everything by the absolute value of sine of theta. So the next step I'm gonna do is take the reciprocal of everything. I'll rewrite it over here. Jerry Nilsson.

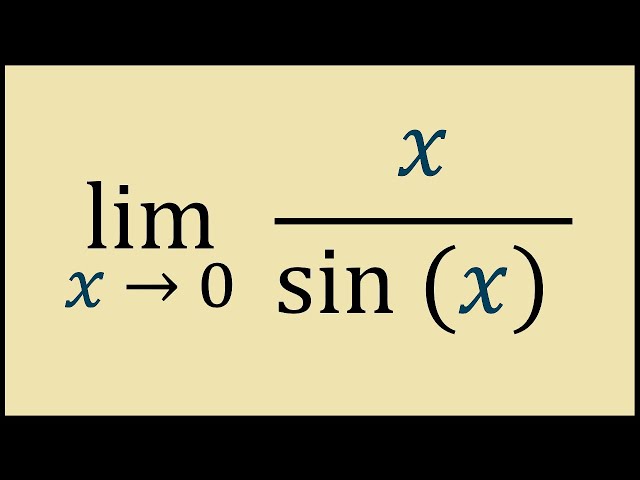
You are not right. Let's discuss. Write to me in PM.
Excuse, that I interrupt you, would like to offer other decision.