Laplace transform of unit step function
Online Calculus Solver ». IntMath f orum ». In engineering applications, we frequently encounter functions whose values change abruptly at specified values of time t.
Online Calculus Solver ». IntMath f orum ». We saw some of the following properties in the Table of Laplace Transforms. We write the function using the rectangular pulse formula. We also use the linearity property since there are 2 items in our function. This is an exponential function see Graphs of Exponential Functions. From trigonometry , we have:.
Laplace transform of unit step function
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Properties of the Laplace transform. About About this video Transcript. Introduction to the unit step function and its Laplace Transform. Created by Sal Khan. Want to join the conversation? Log in. Sort by: Top Voted. Posted 11 years ago.
All you're left with is a function of s. We need the linearity property. It is the function f that is varying.
To productively use the Laplace Transform, we need to be able to transform functions from the time domain to the Laplace domain. We can do this by applying the definition of the Laplace Transform. Our goal is to avoid having to evaluate the integral by finding the Laplace Transform of many useful functions and compiling them in a table. Thereafter the Laplace Transform of functions can almost always be looked by using the tables without any need to integrate. A table of Laplace Transform of functions is available here.
Online Calculus Solver ». IntMath f orum ». We saw some of the following properties in the Table of Laplace Transforms. We write the function using the rectangular pulse formula. We also use the linearity property since there are 2 items in our function. This is an exponential function see Graphs of Exponential Functions.
Laplace transform of unit step function
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Properties of the Laplace transform. About About this video Transcript. Introduction to the unit step function and its Laplace Transform. Created by Sal Khan. Want to join the conversation? Log in.
Duminos roblox
Let me pause it. The issue here is in the normal way we write laplace transforms, the variable of integration is implied. Shifted unit step function Rectangular pulse. In fact, at this point, this unit step function, it has no use anymore. The question then is, did you tell it not to, and if you did, how? Or am I looking at this incorrectly? But now you understand at least what it is and why it essentially shifts a function and zeroes out everything before that point. That's our unit step function, and we want it to jump to 2. So in this case, it's the Laplace transform of sine of t. This is f of t. So this everything's going to be zeroed out until we get to c. It might have gone something like this. Problem Solver provided by Mathway. This is how we will commonly write our functions. In the video, he never takes the Laplace transform of just the unit step function.
Online Calculus Solver ». IntMath f orum ». In engineering applications, we frequently encounter functions whose values change abruptly at specified values of time t.
Log in. And it's the integral of e to the minus s, but now instead of a t, we have the substitution. All you're left with is a function of s. If we go up one more above c, so let's say this is one more above c, so we get to this point, if t is c plus 1, then when you put c plus 1 minus c, you just have f of 1, and f of 1 is really just this point right here. Learn More. Home » Laplace Transforms » 4. Disclaimer: IntMath. So how could we do that? Home » Laplace Transforms » 1a. And also, if we took the derivative of both sides of this, or I guess the differential, you would get dx is equal to dt. And then we'll call this f of t. I was going down the other road when I did the substitution first, which would have worked, but I think the argument as to why I could have changed the boundaries would've been a harder argument to make.

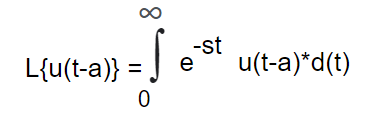
You have hit the mark. It is excellent thought. It is ready to support you.