Khan academy finite element method
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Linear algebra. Unit 1. Unit 2. Unit 3.
Khan academy finite element method
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Modeling situations with differential equations. About About this video Transcript. Differential equations are equations that relate a function with one or more of its derivatives. This means their solution is a function! Learn more in this video. Want to join the conversation? Log in. Sort by: Top Voted. Posted 9 years ago. At
And is this process of trial and error common as you continue to progress towards more advanced theories like this one? Previous 1. Well we have already proven that it works for 1 so we can assume it works for 1.
Personalise your OpenLearn profile, save your favourite content and get recognition for your learning. Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available. The basic principles underlying the FEM are relatively simple.
The finite element method FEM is a powerful technique originally developed for numerical solution of complex problems in structural mechanics , and it remains the method of choice for complex systems. In the FEM, the structural system is modeled by a set of appropriate finite elements interconnected at discrete points called nodes. Elements may have physical properties such as thickness, coefficient of thermal expansion , density , Young's modulus , shear modulus and Poisson's ratio. The origin of finite method can be traced to the matrix analysis of structures [1] [2] where the concept of a displacement or stiffness matrix approach was introduced. Finite element concepts were developed based on engineering methods in s. The finite element method obtained its real impetus in the s and s by John Argyris , and co-workers; at the University of Stuttgart , by Ray W. Straight or curved one-dimensional elements with physical properties such as axial, bending, and torsional stiffnesses. This type of element is suitable for modeling cables, braces, trusses, beams, stiffeners, grids and frames. Straight elements usually have two nodes, one at each end, while curved elements will need at least three nodes including the end-nodes.
Khan academy finite element method
Forgot password? New user? Sign up. Existing user? Log in. Already have an account? Log in here.
Sarathkumar
With these sum induction problems, it is typically best to group the first k addends and replace them with your assumed form. I asked my math teacher and he said it should be real We are going to prove that this formula right over here, this expression right over here applies for the case of 1, when n is 1. Unit 1: Vectors and spaces. This is the same thing as k plus 1, that's this part right over here. Thomas B. Howard Bradley. And the reason why this works is - Let's say that we prove both of these. Is this something obtained simply through observation that if you take a number and multiply it by the integer of adding one to it, and dividing by two that you obtain the sum of the integers up to and including itself; trial and error? This is "the most obvious" root. So if you assume it worked for 1 then it can work for 2. The basic principles underlying the FEM are relatively simple. So let me write this as maybe an algebraic equation that you're familiar with. And if we take the second derivative of y one, this is equal to the same exact idea, the derivative of this is three times negative three is going to be nine e to the negative three x. Differential equations are much more advanced, and should be studied once you have a firm knowledge of both differential calculus and integral calculus.
If you're seeing this message, it means we're having trouble loading external resources on our website.
Second derivative, one of the profound things of the exponential function, the second derivative here is also e to the x. So we are going to have k times k plus 1 plus 2 times k plus 1. Comment Button navigates to signup page. Posted 4 years ago. Unit 1: Vectors and spaces. Differential Equations Demystified covers all of the D. But I'm not sure that I'm really getting the hang of it, though. Why do we use the character "k" and not stick with "n", would the answer not be the same, and furthermore, would a better name for this process not simply be "substitution"? This is the same thing as k plus 1, that's this part right over here. Or everything above some threshold.

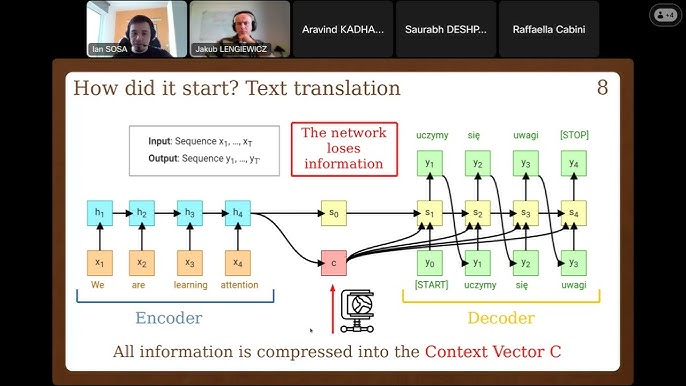
The same...