How to solve sas triangle

Two sides and an angle are enough to uniquely define a triangle: learn why and how to calculate the remaining quantities in a triangle with our SAS triangle calculator. Triangles are rather special polygons.

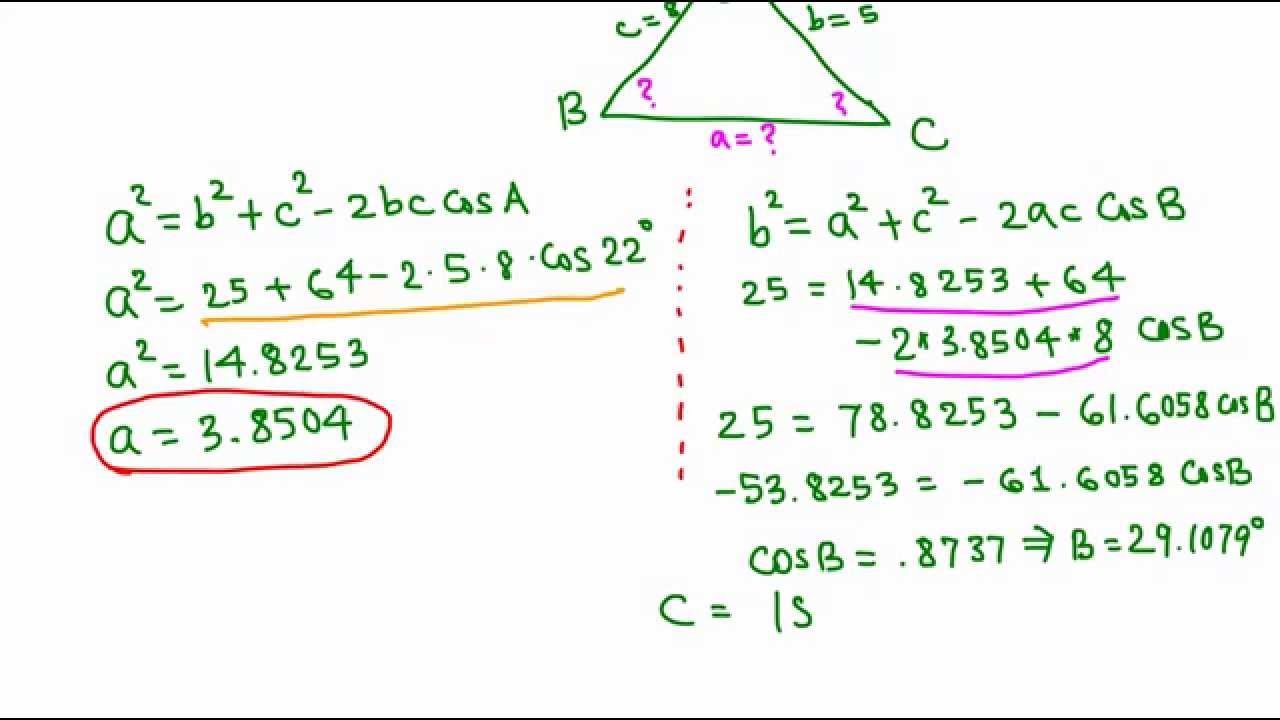
Oblique triangles do not have any right angles. When solving oblique triangles, we must first know the measure of at least one leg and the measure of the other two parts of the oblique triangle: two angles, two legs, or one side and one angle. In simple words, we can get a lot of different combinations when solving the oblique triangles. One of these combinations or attributes is the SAS triangle. Figure illustrates a triangular combination which is known as a SAS triangle. When we know the measure of two sides and the included angle, we can apply a three-step method to solve a SAS triangle: using the Law of Cosines, using the Law of Sines, and determining the measure of the third angle.

How to solve sas triangle

SAS triangles are triangles where two sides and the angle between them are known. Find the missing angles and the side in the given SAS triangle. Find the missing angles and the side in the given triangle. The given triangle is an SAS triangle. Identify which pair of triangles below illustrates an SAS relationship to prove the triangles are congruent. The method discussed above is just an extension of the general formula for determining the area of a triangle. Find the area of the given triangle. Your email address will not be published. Save my name, email, and website in this browser for the next time I comment. About us Contact us. All rights reserved. Reproduction in whole or in part without permission is prohibited. Table of Contents.

Reproduction in whole or in part without permission is prohibited.

.

Two triangles are congruent if two sides and the included angle of one are equal respectively to two sides and the included angle of the other,. Similarly for 2 and 3. Thus, if the triangles are congruent, the correspondence must be. The following procedure was used to measure the d. We have. The SAS Theorem is Proposition 4 in Euclid's Elements , Both our discussion and Suclit's proof of the SAS Theoremimplicitly use the following principle: If a geometric construction is repeated in a different location or what amounts to the same thing is "moved" to a different location then the size and shape of the figure remain the same, There is evidence that Euclid used this principle reluctantly, and many mathematicians have since questioned its use in formal proofs, They feel that it makes too strong an assumption about the nature of physical space and is an inferior form of geometric reasoning. Bertrand Russell - , for example, has suggested that we would be better off assuming the SAS Theorem as a postulate , This is in fact done in a system of axioms for Euclidean geometry devised by David Hilbert - , a system that has gained much favor with modern mathematicians. Hilbert was the leading exponent of the "formalist school," which sought to discover exactly what assumptions underlie each branch of mathematics and to remove all logical ambiguities, Hilbert's system, however, is too formal for an introductory course in geometry,.

How to solve sas triangle

Two sides and an angle are enough to uniquely define a triangle: learn why and how to calculate the remaining quantities in a triangle with our SAS triangle calculator. Triangles are rather special polygons. Undeformable, ubiquitous, neverending source of mathematical theorems, hell, they constantly appear in trigonometry, too! One of the reasons for these peculiarities is that sides and vertices of a triangle are related by strong constraints. Also, the small number of vertices makes it possible to fix the distances in a triangle by assigning the values of just two sides. Once the values are set, the triangle is uniquely identified. We will talk later about another important concept in the study of triangles, congruence.

Hombre busca hombre culiacán

Other similar combinations don't guarantee congruence. Once the values are set, the triangle is uniquely identified. In simple words, we can get a lot of different combinations when solving the oblique triangles. The latter case may allow for multiple solutions; thus, we are not going to deal with it in this tool. Find the area of the given triangle. The combination of two adjacent sides and the angle between them defines at the same time both the shape and the scale of the triangle. The combination SSA, for example, allows the creation of both acute and obtuse angles with the same set of initial values. SAS Triangle. Leave a Reply Cancel reply Your email address will not be published. Last modified on August 3rd, We will apply the three-step method to solve a SAS triangle. With such a set of values, the only thing we can do is connect the ends of the sides and close the triangle: there is no opportunity to change the shape because of the angle or scale because of the given length of two sides. Tangent Check out this tangent calculator if you want to calculate the tangent of any angle. Identify which pair of triangles below illustrates an SAS relationship to prove the triangles are congruent. Embed Share via.

Unfortunately, while the Law of Sines enables us to address many non-right triangle cases, it does not help us with triangles where the known angle is between two known sides, a SAS side-angle-side triangle, or when all three sides are known, but no angles are known, a SSS side-side-side triangle. In this section, we will investigate another tool for solving oblique triangles described by these last two cases. The tool we need to solve these types of problems is the Law of Cosines , which defines the relationship among angle measurements and side lengths in oblique triangles.

Triangles are rather special polygons. The combination SSA, for example, allows the creation of both acute and obtuse angles with the same set of initial values. What will be the distance between the airplanes after three hours? Other similar combinations don't guarantee congruence. What if you don't have a SAS triangle? If you define the values of two adjacent sides and the angle between them you've given enough material to calculate everything in a triangle. Practice Questions 1. Figure illustrates a triangular combination which is known as a SAS triangle. Find the missing angles and the side in the given SAS triangle. We can calculate the area of a triangle if the given quantities are two adjacent sides and the angle between them with a particular SAS triangle formula for the area:. Table of contents: What's so special about triangles? A SAS triangle is uniquely defined. All rights reserved. Which, rather conveniently, uses the original quantities to find the value. Tangent Check out this tangent calculator if you want to calculate the tangent of any angle.