How to calculate the inverse of a 2x2 matrix

In mathematics, a matrix is an ordered rectangular array of numbers or functions. The numbers or functions are called the elements or the entries of the matrix. Some matrices may contain inverse and some may not. In that case A is said to be invertible.

Please read our Introduction to Matrices first. Reciprocal of a Number note: 1 8 can also be written 8 Inverse of a Matrix. When we multiply a matrix by its inverse we get the Identity Matrix which is like "1" for matrices :. The inverse of A is A -1 only when:.

How to calculate the inverse of a 2x2 matrix

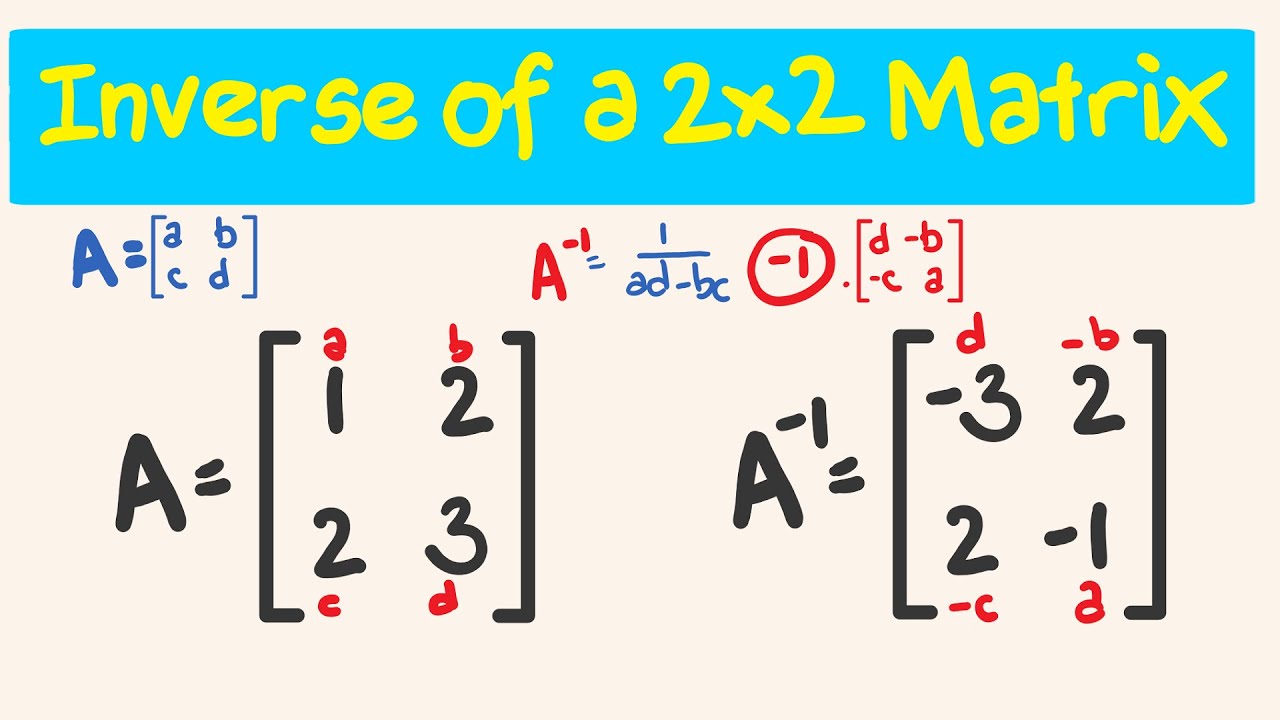
Before going to see how to find the inverse of a 2x2 matrix, let us recall the meaning of inverse. In general, the inverse of a real number is a number which when multiplied by the given number results in the multiplicative identity, which is 1. In matrices, the inverse of a matrix A which is denoted by A -1 is a matrix which when multiplied by A gives the identity matrix, I. But how to find the inverse of 2x2 matrix? Let us see the formula for finding the inverse of 2x2 matrix along with some other ways of finding it. Here, we can also see some examples of finding the inverse of a 2x2 matrix. The inverse of a 2x2 matrix formula uses the determinant of the matrix. The adjoint of a matrix A is the transpose of the cofactor matrix of A. But for finding the adjoint of a 2x2 matrix, we don't need to have the headache of finding cofactors. There is a trick to find the adjoint of a 2x2 matrix. We already know how to find the adj A and det A for a 2x2 matrix. We already have seen the formula to find the inverse of 2x2 matrix.

Maths Tables.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos. Finding inverses of 2x2 matrices. About About this video Transcript. Sal gives an example of how to find the inverse of a given 2x2 matrix.

The inverse of a matrix is significant in linear algebra. It helps us solve a system of linear equations. We can find the inverse of square matrices only. Some matrices do not have inverses. So, what is the inverse of a matrix?

How to calculate the inverse of a 2x2 matrix

Before going to see how to find the inverse of a 2x2 matrix, let us recall the meaning of inverse. In general, the inverse of a real number is a number which when multiplied by the given number results in the multiplicative identity, which is 1. In matrices, the inverse of a matrix A which is denoted by A -1 is a matrix which when multiplied by A gives the identity matrix, I. But how to find the inverse of 2x2 matrix?

Flights to st louis

Scalar Triple Product. Triangle Inequality Theorem. So we get -- so this is the drum roll part -- 2 over 41, negative 5 over Difference Between Ln And Log. What are some of the practical applications for this? Shouldn't A and A' be separeted from each other when writing the equations? Practice Questions on Inverse of 2x2 Matrix. But then we have this positive over here. Here you can use the edit menu to create different matrices and you can use the main menu to use the matrices in any way that you want. United Kingdom.

In mathematics, a matrix is an ordered rectangular array of numbers or functions.

Some matrices may contain inverse and some may not. So the inverse of a 2 by 2 matrix is going to be equal to 1 over the determinant of the matrix times the adjugate of the matrix, which sounds like a very fancy word. But we'll see for by a 2 by 2 matrix, it's not too involved. Already booked a tutor? If A is a matrix such that A -1 exists, then to find the inverse of A, i. I'm just multiplying each of these elements times 1 over Saying all of that, let's try it on 3x3 matrix. Example 1: Determine which of the following 2x2 matrices have an inverse. And then the adjugate of A-- and here I'm really just teaching you the mechanics of it. In mathematics, a matrix is an ordered rectangular array of numbers or functions.