How to calculate surface area of a square pyramid

This online calculator will calculate the various properties of a square pyramid given 2 known variables. The square pyramid is a special case of a pyramid where the base is square. It is a regular pyramid since it has a square base which is a regular polygon.

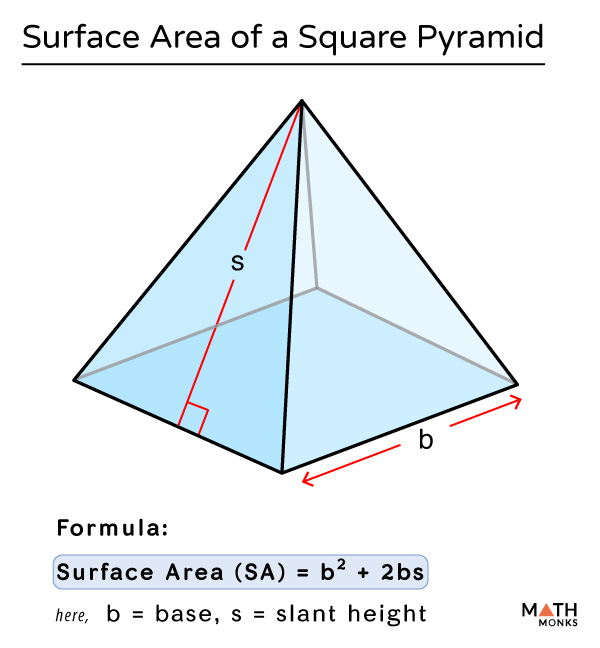
In this section, we will learn about the surface area of a square pyramid. A pyramid is a 3-D object whose all side faces are congruent triangles and whereas its base can be any polygon. One side of each of these triangles coincides with one side of the base polygon. A square pyramid is a pyramid whose base is a square. The pyramids are named according to the shape of their bases. Just like other three-dimensional shapes, a square pyramid also has two types of areas. Let us learn about the surface area of a square pyramid along with the formula and a few solved examples here.

How to calculate surface area of a square pyramid

Are you in search of a surface area of a square pyramid calculator to estimate all types of areas of the Great pyramid?! If yes, you're in the right place. You can calculate the total surface area, base area, lateral surface area, and face area of any square pyramid using our tool. We also discuss how to find the surface area of a square pyramid using slant height and base length and how to calculate surface area using slant height and base perimeter. You can also find answers to some interesting numerical problems like the surface area of a pyramid of Giza and the amount of groundsheet required for any tent. The base of a square pyramid is a square. Hence, the base area of the square pyramid of base edge a is a 2. First of all, let's explain what the lateral area of a square pyramid is. The lateral surface area or lateral area of a square pyramid is the total area of its 4 triangular faces. We calculate the lateral area as:. The face area of a square pyramid is the area of one of its four triangular faces. We calculate the area of a triangular face, the face area FA , using the formula:. The area of a triangle is half of the product of its base length a and height l :. Therefore, the area of four triangular faces or the lateral surface area of the square pyramid is:. Thus, the lateral surface area LSA of the square pyramid of slant height l is.

In a pyramid, the base is connected to all the faces of the pyramid.

In mathematics, a pyramid is a three-dimensional geometric structure with a polygonal base and triangular faces equal to the number of sides in the base. The triangular faces or lateral surfaces of a pyramid meet at a single point known as the apex or the vertex. In a pyramid, the base is connected to all the faces of the pyramid. Pyramids are classified into different types, such as triangular pyramids, square pyramids, rectangular pyramids, pentagonal pyramids, hexagonal pyramid, etc. A square pyramid is a pyramid that has a square base and four triangular faces that meet at a point at the top called the apex.

A pyramid has one base made of any shape and the rest of the faces are triangles. The pyramid is named by the shape of its base. I create online courses to help you rock your math class. Read more. This is a triangular pyramid and its net. The net of a triangular pyramid has three triangular faces and one triangular base.

How to calculate surface area of a square pyramid

The pyramid has a lot of possible base shapes, from the simple square seen in Egyptian pyramids to hexagonal deck prisms, used in sailing ships of olden days, to cast light into lower decks. Because you can find pyramids with triangular, rectangular, square, pentagonal, hexagonal and octagonal bases, you could be asked to perform mathematical exercises such as these:. Which will always be larger, the lateral area of a pyramid or the total surface area of a pyramid? Calculate the total surface area of a rectangular pyramid with a base 20 meters by 15 meters and a height of 50 meters. What is the total surface area of a hexagonal pyramid with slanted sides 7 yards in length and each side of the base measuring 3 yards? Find the lateral area of a pyramid with a square base, a height of feet , and a slanted side length of feet. Compare the total surface area of a triangular pyramid with base sides 30 cm and slant height of its three sides 60 cm to the total surface area of a square pyramid with base sides 20 cm and slant height of its four sides 50 cm. These are all challenging problems, becoming more complex as they go. Fortunately, several formulas exist to help you deal with every type of pyramid, no matter the polygon forming its base.

Night court john larroquette

Campus Experiences. If you've found an issue with this question, please let us know. A square pyramid is also referred to as a pentahedron as it has five faces, including a square base and four triangular faces lateral faces. Example 1: Find the surface area of a square pyramid of slant height 15 units and base length 12 units. Follow CalculatorSoup:. This article is being improved by another user right now. Additional Information. Explanation : To find surface area of a pyramid, simply find the surface area of each of the faces and add them together. To find the lateral area of a square pyramid, find the area of one side face triangle and multiply it by 4. Hanley Rd, Suite St. We need to calculate the slant height of the triangular face by using the Pythagorean Theorem:.

Last Updated: November 24, This article was co-authored by Grace Imson, MA.

Pyramids are classified into different types, such as triangular pyramids, square pyramids, rectangular pyramids, pentagonal pyramids, hexagonal pyramid, etc. Hanley Rd, Suite St. The area of a square is given by: The area of a triangle is: The given height of 12 in is from the vertex to the center of the base. In other words the point at the top of the pyramid is directly above the center point of the square base. It is a regular pyramid since it has a square base which is a regular polygon. Engineering Exam Experiences. Open In App. This online calculator will calculate the various properties of a square pyramid given 2 known variables. Become a problem-solving champ using logic, not rules. You can find a few practice questions in the end.