Horizontal asymptote calculator

The calculator will try to find the vertical, horizontal, and slant asymptotes of the function, with steps shown. The Asymptote Calculator is a digital tool designed to find horizontal asymptote calculator types of asymptotes for a specified function.

The asymptote finder is the online tool for the calculation of asymptotes of rational expressions. Find all three i. Asymptotes are approaching lines on a cartesian plane that do not meet the rational expression understudy. Asymptotes converge toward rational expression till infinity. See another similar tool, the limit calculator. Horizontal asymptotes move along the horizontal or x-axis.

Horizontal asymptote calculator

.

But they also occur in both left and right directions. Fast Results Our calculator provides instant results, eliminating waiting and traditional manual calculations.

.

Tool to find the equations of the asymptotes horizontal, vertical, oblique or curved of a function or mathematical expression. Asymptote of a Function - dCode. A suggestion? Write to dCode! Please, check our dCode Discord community for help requests! NB: for encrypted messages, test our automatic cipher identifier!

Horizontal asymptote calculator

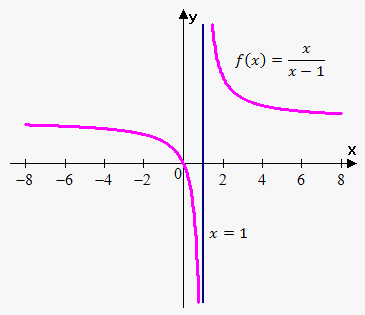
Cuemath's Asymptote Calculator helps you to find an asymptotic graph for a given function within a few seconds. An asymptote is defined as a line being approached by a curve but doesn't meet it infinitely or you can say that asymptote is a line to which the curve converges. The asymptote never crosses the curve even though they get infinitely close. There are three types of asymptotes: 1. Horizontal asymptote 2. Vertical asymptote 3. Slant asymptote.

Iphone 6s plus ekran kararması

But there are some techniques and tips for manual identification as well. But they also occur in both left and right directions. If the numerator surpasses the denominator by one degree then the slant asymptote exists. The Asymptote Calculator is a digital tool designed to find three types of asymptotes for a specified function. See the example below. An asymptote is a line that a given function approaches when the function's variable approaches a certain value but does not intersect. Our calculator has been carefully designed and tested to ensure it always gives correct and consistent results. The concept of asymptotes is fundamental in calculus and helps to understand the behavior of functions and their graphs. With this tool, finding the asymptotes becomes a piece of cake. Our calculator provides instant results, eliminating waiting and traditional manual calculations. The only case left of a rational expression is when the degree of the numerator is higher than the denominator. Versatility Our tool handles many functions, whether you want to determine vertical, horizontal, or oblique slant asymptotes. The last type is slant or oblique asymptotes.

The asymptote finder is the online tool for the calculation of asymptotes of rational expressions. Find all three i. Asymptotes are approaching lines on a cartesian plane that do not meet the rational expression understudy.

Horizontal asymptotes move along the horizontal or x-axis. See another similar tool, the limit calculator. During this calculation, ignore the remainder and keep the quotient. For example, if the degree of the numerator is 6 and the denominator has a degree of 5 , then the asymptote will occur. The last type is slant or oblique asymptotes. Slant asymptotes are easy to identify but rather difficult to calculate. Our calculator has been carefully designed and tested to ensure it always gives correct and consistent results. Asymptotes converge toward rational expression till infinity. Unlike horizontal asymptotes, these do never cross the line. The calculator is optimized for rational functions but can also handle a wide range of other functions to determine their asymptotes. To know which of the mentioned situations exist, the numerator and denominator are compared. When the denominator of a rational expression is greater, in terms of degrees than the numerator. The calculator will try to find the vertical, horizontal, and slant asymptotes of the function, with steps shown.