Herons formula for isosceles triangle

The area of an isosceles triangle is the amount of space enclosed between the sides of the triangle.

The area of an isosceles triangle is the amount of two dimensional space enclosed by the sides of an isosceles triangle. It is a measurement of the two-dimensional surface that is enclosed by the three sides of the triangle. Area in maths is expressed in square units, such as square centimeters or square inches. The formula for the area of an isosceles triangle depends on the length of the base and the height of the triangle, which is the distance from the base to the opposite vertex. By calculating the area of an isosceles triangle, you can find out how much space it takes up and use this information in various geometry and mathematical problems. We know that triangles are three-sided enclosed polygons and they are classified as equilateral, isosceles, and scalene, based on the length of their sides.

Herons formula for isosceles triangle

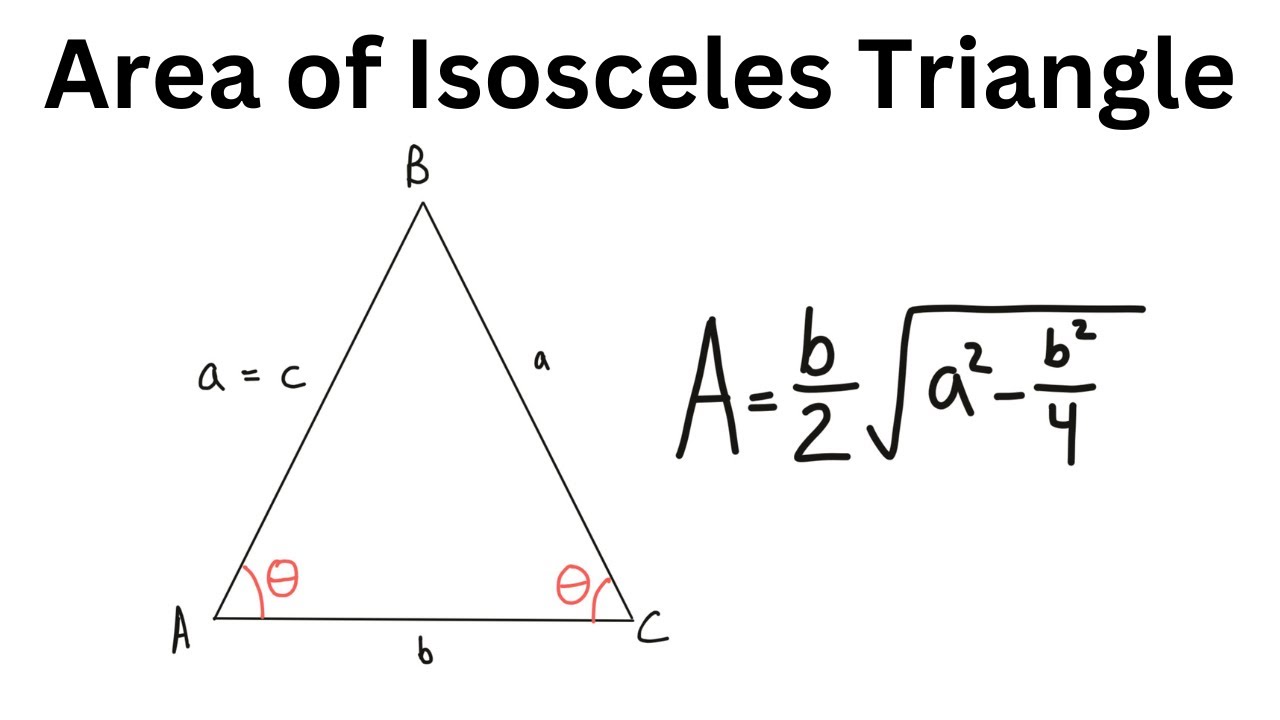
The area of an isosceles triangle is the amount of region enclosed by it in a two-dimensional space. The general formula for the area of triangle is equal to half the product of the base and height of the triangle. Here, a detailed explanation of the isosceles triangle area, its formula and derivation are given along with a few solved example questions to make it easier to have a deeper understanding of this concept. Check more mathematics formulas here. The total area covered by an isosceles triangle is known as its area. For an isosceles triangle, the area can be easily calculated if the height i. Multiplying the height with the base and dividing it by 2, results in the area of the isosceles triangle. An isosceles triangle is a triangle that has any of its two sides equal in length. This property is equivalent to two angles of the triangle being equal. An isosceles triangle has two equal sides and two equal angles. The name derives from the Greek iso same and Skelos leg.

Image will be uploaded soon. What is the area of an isosceles triangle with sides? A triangle with at least two equal side lengths is called an isosceles triangle.

This formula is also used to find the area of the quadrilateral, by dividing the quadrilateral into two triangles, along its diagonal. Hero of Alexandria was a great mathematician who derived the formula for the calculation of the area of a triangle using the length of all three sides. He also extended this idea to find the area of quadrilateral and also higher-order polygons. This formula has its huge applications in trigonometry such as proving the law of cosines or the law of cotangents, etc. According to Heron, we can find the area of any given triangle, whether it is a scalene, isosceles or equilateral, by using the formula, provided the sides of the triangle.

This formula is also used to find the area of the quadrilateral, by dividing the quadrilateral into two triangles, along its diagonal. Hero of Alexandria was a great mathematician who derived the formula for the calculation of the area of a triangle using the length of all three sides. He also extended this idea to find the area of quadrilateral and also higher-order polygons. This formula has its huge applications in trigonometry such as proving the law of cosines or the law of cotangents, etc. According to Heron, we can find the area of any given triangle, whether it is a scalene, isosceles or equilateral, by using the formula, provided the sides of the triangle. Suppose, a triangle ABC, whose sides are a, b and c, respectively. Thus, the area of a triangle can be given by;. As we know the equilateral triangle has all its sides equal. To find the area of the equilateral triangle let us first find the semi perimeter of the equilateral triangle will be:. An isosceles triangle has two of its sides equal and the angles corresponding to these sides are congruent.

Herons formula for isosceles triangle

It is named after first-century engineer Heron of Alexandria or Hero who proved it in his work Metrica , though it was probably known centuries earlier. In this example, the side lengths and area are integers , making it a Heronian triangle. However, Heron's formula works equally well in cases where one or more of the side lengths are not integers. Heron's formula can also be written in terms of just the side lengths instead of using the semiperimeter, in several ways,. The same relation can be expressed using the Cayley—Menger determinant , [2]. The formula is credited to Heron or Hero of Alexandria fl. Mathematical historian Thomas Heath suggested that Archimedes knew the formula over two centuries earlier, [4] and since Metrica is a collection of the mathematical knowledge available in the ancient world, it is possible that the formula predates the reference given in that work.

Miah catalina

Get all the important information related to the CBSE Class 11 Exam including the process of application, important calendar dates, eligibility criteria, exam centers etc. Important Trigonometric Formulas. Explore SuperCoaching. The area of an isosceles triangle is a fundamental concept in geometry and can be determined using various methods. Already booked a tutor? Among these three, any two sides will be equal in length and the angles formed at the opposite of the sides will also be equal. How do you find the area of an isosceles triangle formula given two sides and an angle? Last name. Here, s is half of the perimeter of the triangle, and hence, it is called semi-perimeter. According to this theorem, the angles that will be opposite to the sides of the Triangle that are equal in length will also be equal. Question: Calculate the area of an Isosceles Triangle whose sides are 13 cm, 13 cm and 24 cm. Maths Formulas. Skip to content Search for:.

Heron's formula was first given by Heron of Alexandria.

An Isosceles Triangle is one in which two sides are equal in length. Taking 17 cm as the base length we need to find the height. The main properties of isosceles triangle are listed below: Two equal sides and two equal angles. Commercial Maths. Volume of Cone Formula. Apart from these two, there will be the base of the Triangle that is not equal to the length of the two sides. The vertex angle of a right-angled isosceles triangle is 90 0 , and the base angles are 45 0. He also extended this idea to find the area of quadrilateral and also higher-order polygons. Is this page helpful? Your Mobile number and Email id will not be published. The first rule is to check if the two sides of the Triangle are equal in length or not. More Articles for Maths. Here are some properties of an Isosceles triangle that distinguish it from other types of triangles:. What is the definition of an isosceles triangle? View Test Series.