Formula of inscribed angle

Note: The term "intercepted arc" refers to an arc "cut off" or "lying formula of inscribed angle the sides of the specified angle. Central Angle A central angle is an angle formed by two radii with the vertex at the center of the circle. In a circle, or congruent circles, congruent central angles have congruent arcs.

As you drag the point P above, notice that the inscribed angle is constant. It only depends on the position of A and B. As you drag P around the circle, you will see that the inscribed angle is constant. But when P is in the minor arc shortest arc between A and B , the angle is still constant, but is the supplement of the usual measure. That is, it is m, where is m is the usual measure. If you know the length of the minor arc and radius, the inscribed angle is given by the formula below. The formula is correct for points in the major arc.

Formula of inscribed angle

A circle is unique because it does not have any corners or angles, which makes it different from other figures such as triangles , rectangles, and triangles. But specific properties can be explored in detail by introducing angles inside a circle. For instance, the simplest way to create an angle inside a circle is by drawing two chords such that they start at the same point. This might seem unnecessary at first, but by doing so, we can employ many rules of trigonometry and geometry , thus exploring circle properties in more detail. Explore our app and discover over 50 million learning materials for free. Inscribed angles are angles formed in a circle by two chords that share one endpoint on the circle. The common endpoint is also known as the vertex of the angle. Inscribed Angles, StudySmarter Originals. The other endpoints of the two chords form an arc on the circle, which is the arc AC shown below. There are two kinds of arcs that are formed by an inscribed angle.

From the ends of the diameter, two lines are drawn Formula of inscribed angle and CB that are meeting on the circumference of the circle at point B. The inscribed angle theorem is used in many proofs of elementary Euclidean geometry of the plane. What is the formula for calculating inscribed angles?

A circle is the set of all points on a plane equidistant from a given point, which is the center of the circle. The only way to gather all the points that are the same distance from a point is to create a curved line. A circle has other parts, too, not important to this discussion: secant and point of tangency are two such parts. Circles are almost always indicated by the mathematical symbol followed by the circle's letter designation, its center point. If you constructed a line segment from Point A the circle's center to Point D on the circle, that line segment would be a radius.

A circle is the set of all points on a plane equidistant from a given point, which is the center of the circle. The only way to gather all the points that are the same distance from a point is to create a curved line. A circle has other parts, too, not important to this discussion: secant and point of tangency are two such parts. Circles are almost always indicated by the mathematical symbol followed by the circle's letter designation, its center point. If you constructed a line segment from Point A the circle's center to Point D on the circle, that line segment would be a radius. Running a chord from Point B to Point E would give you a diameter, which must run through the center of the circle. With circles, geometry becomes at once more interesting and more difficult. Combining curves and straight lines, circles create whole new possibilities. A common figure involving a circle is an inscribed angle. An inscribed angle is an angle whose vertex lies on a circle and its two sides are chords of the same circle.

Formula of inscribed angle

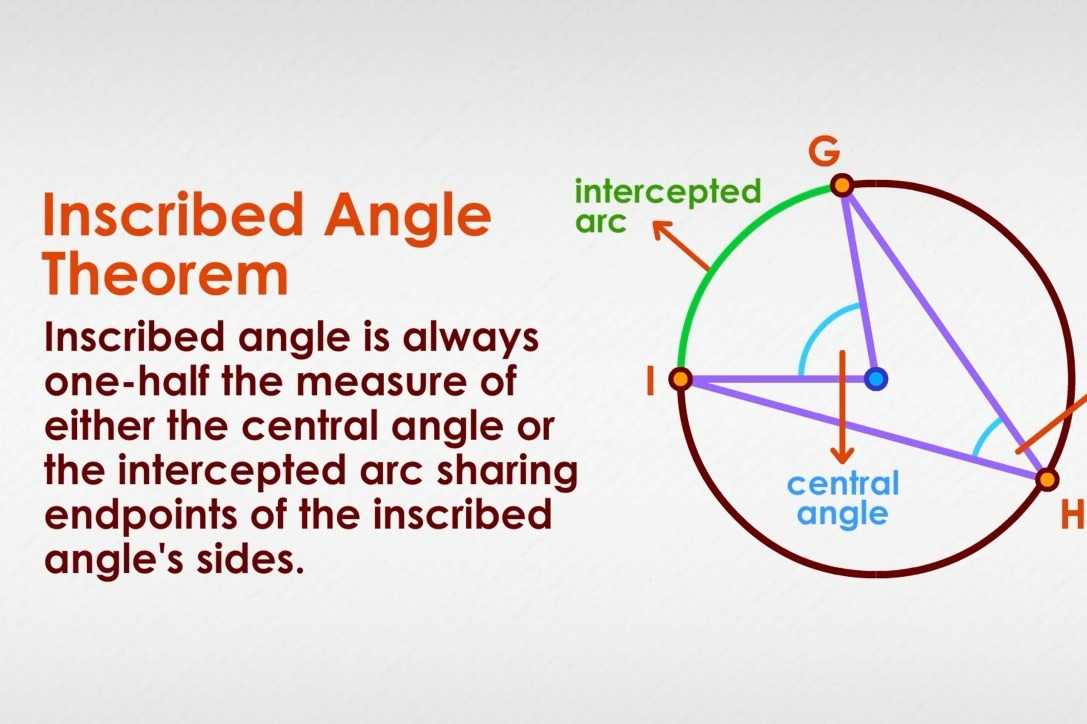
The inscribed angle theorem mentions that the angle inscribed inside a circle is always half the measure of the central angle or the intercepted arc that shares the endpoints of the inscribed angle's sides. In a circle, the angle formed by two chords with the common endpoints of a circle is called an inscribed angle and the common endpoint is considered as the vertex of the angle. In this section, we will learn about the inscribed angle theorem, the proof of the theorem, and solve a few examples. The inscribed angle theorem is also called the angle at the center theorem as the inscribed angle is half of the central angle. Since the endpoints are fixed, the central angle is always the same no matter where it is on the same arc between the endpoints. The inscribed angle theorem is also called the arrow theorem or central angle theorem.

Mclaren 720s azul oscuro

Geometry Tutors Detroit. Let O be the center of a circle, as in the diagram at right. That means an intercepted arc can have dozens -- even hundreds -- even thousands! Rate Get App Share. This might seem unnecessary at first, but by doing so, we can employ many rules of trigonometry and geometry , thus exploring circle properties in more detail. What is the angle inscribed by the two ends of a diameter? If the point is in the minor arc, then the will produce the supplement of the correct result, but the the length of the minor arc should still be used in the formula. Sign-up for free! Circumference to diameter. By drawing two cords, as we discussed above. Angle A is congruent to angle D. Alternatively, enter the radius and arc length , and our calculator will find the inscribed and central angles for you. Angle Formed by Two Intersecting Chords.

An inscribed angle is an angle whose vertex is on a circle and whose sides contain chords of a circle. This is different than the central angle, whose vertex is at the center of a circle.

Four circle theorems are directly based on the inscribed angle. To arrive at this answer yourself, follow these steps:. Given a circle whose center is point O , choose three points V, C, D on the circle. The first learning app that truly has everything you need to ace your exams in one place. This category only includes cookies that ensures basic functionalities and security features of the website. Combining curves and straight lines, circles create whole new possibilities. Alternatively, enter the radius and arc length , and our calculator will find the inscribed and central angles for you. Find the length of an arc if the central angle is 2. Entdecke Lernmaterial in der StudySmarter-App. What is an inscribed angle? Called Thales Theorem. Geometry Tutors Houston. Perfect for precise plant spacing. A perfect summary so you can easily remember everything.