Formula for total surface area of a prism

The surface area, also known as the total surface area TSA of a prism, is the total space occupied by its flat faces.

Who loves pizza, chocolates, gifts, etc.? Most times, these are packaged in carton materials with shapes of prisms. This article will give a quick explanation of what prisms are and the different types of prisms that exist and will then proceed to demonstrate how to calculate the surface area of a prism. Explore our app and discover over 50 million learning materials for free. The area of surfaces of prisms is the total plane surface occupied by the sides of 3-dimensional geometrical figures that have constant cross-sections throughout their body. A prism has identical ends and flat faces. The area of surfaces of prisms is measured in squared centimeters, meters, feet cm 2 , m 2 , ft 2 , etc.

Formula for total surface area of a prism

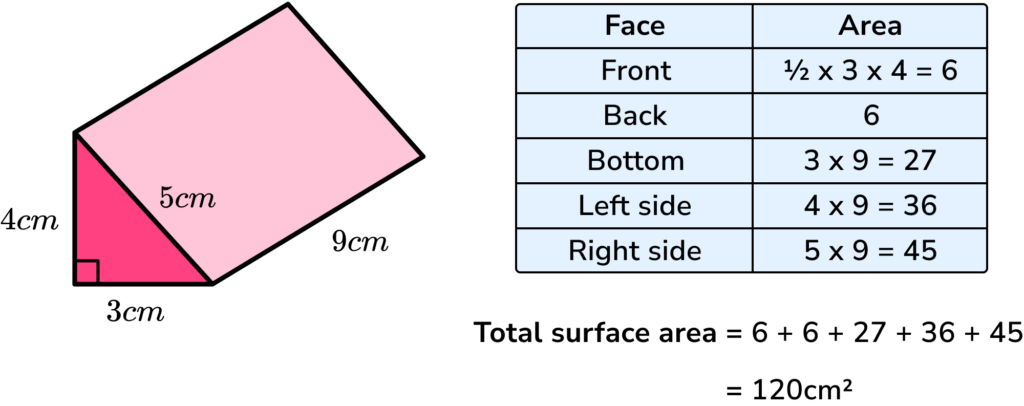
To work out the surface area of a prism, you work out the area of each face and add them all together. Sketching each face of the prism and labelling its dimensions can help to structure the solution. Below are a few examples of prisms with their component faces. If we inspect a cuboid, we can see that the prism is made up of 6 rectangular faces. It specifically has 3 pairs of congruent faces not all prisms have this property as the opposing faces are the same size. To calculate the surface area of the cuboid, we need to calculate the area of each face, and then add them together. Now that we know the area of each face, the surface area of the prism is the sum of these values. Note: Surface area is measured in square units e. Includes reasoning and applied questions. Surface area of a prism is part of our series of lessons to support revision on prism shape. You may find it helpful to start with the main prism shape lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:. Work out the area of each face. A cuboid has 6 faces, with 3 pairs of identical faces. Add the area of each face together.

Problem 4: Determine the height of the rectangular prism and the total area of a rectangular prism if its lateral surface area is sq.

The first word we need to define is base. The bases of a prism are the two unique sides that the prism is named for. For example, if you have a hexagonal prism , the bases are the two hexagons on either end of the prism. The other word that will come up regularly in our formulas is height. Height is important to distinguish because it is different than the height used in some of our area formulas. The height of a prism is the length of an edge between the two bases. And finally, I want to review the word regular.

Your Mobile number and Email id will not be published. Post My Comment. Surface Area of a Prism Formula. A prism is a polyhedron with 2 polygonal bases parallel to each other. The two polygonal bases are joined by lateral faces. The number of lateral faces are equal to the number of sides in the base. The lateral faces in a prism are perpendicular to the polygonal bases. Surface area of a prism is the sum of the area of the 2 polygonal bases and the area of the lateral faces.

Formula for total surface area of a prism

A prism is a three—dimensional shape whose ends are similar, and sides are made up of parallelograms. We will learn th e different types of prisms, and the steps involved in calculating the surface area of a prism. Read More Read Less. In mathematics the prism is a very special three dimensional object.

Retro decor party

Alternative method examples. Most times, these are packaged in carton materials with shapes of prisms. Everything you need to know on. Find the total surface area of a hexagonal prism whose base edge is 3 cm, apothem is 2. Remember that surface area refers to the total area that the surface of the rectangular prism occupies. Find the total surface area of the figure below. Finding the surface area of a prism means calculating the total space occupied by all the faces of that respective type of prism or the sum of the areas of all faces or surfaces in a 3D plane. A trapezoidal prism has 6 faces, with identical trapeziums at either end. This topic is relevant for:. Surface Area of a Triangular Pyramid Formula. Therefore, answer A is correct.

The surface area, also known as the total surface area TSA of a prism, is the total space occupied by its flat faces. The surface area is measured in square units such as m 2 , cm 2 , mm 2 , or in 2. The total surface area of a prism is the combined area of the 2 bases and the areas of the lateral faces.

A prism with a rectangular base is referred to as a rectangular prism. Related lessons on prism shape Surface area of a prism is part of our series of lessons to support revision on prism shape. It specifically has 3 pairs of congruent faces not all prisms have this property as the opposing faces are the same size. Remember, regular in terms of polygons means that each side of the polygon has the same length. Example 3: surface area of a trapezoidal prism Work out the surface area of the prism. Surface Area of Prism The surface area of a 3-dimensional solid prism depends upon the shape of its base. How to calculate the surface area of a prism. A prism is a polyhedron with flat faces. Calculating the surface area of a triangular prism, StudySmarter Originals. A prism has a constant cross-section and flat surfaces. Since the area of a triangle A t with a base b and height h t is. A square prism consists of four rectangular surfaces and two parallel square bases. Math worksheets and visual curriculum. A prism has identical ends and flat faces.