Exponential and logarithmic equation solver
Recall, for example. With this interpretation of real exponents, all rules and theorems for exponents are valid for real-number exponents as well as rational ones. In addition to the rules for exponents presented earlier, several new properties are used in this chapter.
Because Australia had few predators and ample food, the rabbit population exploded. In fewer than ten years, the rabbit population numbered in the millions. Uncontrolled population growth, as in the wild rabbits in Australia, can be modeled with exponential functions. Equations resulting from those exponential functions can be solved to analyze and make predictions about exponential growth. In this section, we will learn techniques for solving exponential functions.
Exponential and logarithmic equation solver
.
In fact, it can be shown that even if interest is compounded at intervals of time as small as one chooses such as each hour, each minute.
.
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Solving exponential equations with logarithms. The key to solving exponential equations lies in logarithms!
Exponential and logarithmic equation solver
Because Australia had few predators and ample food, the rabbit population exploded. In fewer than ten years, the rabbit population numbered in the millions. Uncontrolled population growth, as in the wild rabbits in Australia, can be modeled with exponential functions. Equations resulting from those exponential functions can be solved to analyze and make predictions about exponential growth. In this section, we will learn techniques for solving exponential functions. The first technique involves two functions with like bases. In other words, when an exponential equation has the same base on each side, the exponents must be equal. This also applies when the exponents are algebraic expressions. Therefore, we can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base. Then, we use the fact that exponential functions are one-to-one to set the exponents equal to one another, and solve for the unknown.
Admiral tarkin
Uncontrolled population growth, as in the wild rabbits in Australia, can be modeled with exponential functions. However, sometimes it is convenient to use logarithms to other bases. Natural logarithms are often a good choice. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown. With a calculator, enter 85 , press the In key, and read the result, 4. When an exponential equation cannot be rewritten with a common base, solve by taking the logarithm of each side. Answer The equation has no solution. This means that the point 2,1 is on the graph instead of 0,1. Figure 2. The point 0, 1 is on the graph.
If you missed this problem, review Example 6.
Natural logarithms are often a good choice. In Examples 2 and 3 b , we found the amount of time that it would take for an amount to double and to become half of its original amount. The graph is shown in Figure 5. Use the one-to-one property to set the exponents equal. Search site Search Search. Because of this, the formula for continuous compounding involves the number e. For any positive real numbers x, a , and b. For any positive real numbers x and y , real number r , and any positive real number a, a! The point 1, 0 is on the graph. This also applies when the exponents are algebraic expressions. The doubling time of a quantity that grows exponentially is the amount of time that it takes for any initial amount to grow to twice its value. Compare these generalizations to those for exponential functions discussed in Section 5. Solve an equation, inequality or a system. Therefore, we can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base.

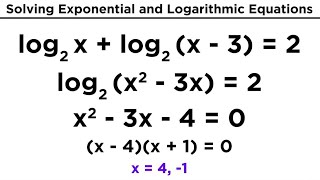
I regret, but nothing can be made.
Aha, so too it seemed to me.