Evaluating the six trigonometric functions

In the Trigonometric Functions section, you will learn how to evaluate trigonometric functions at various angle measures and also graph trigonometric functions. Understanding how to find a reference angle of a given angle is an important skill needed to evaluate trigonometric functions and is reviewed here. Even-odd properties are also reviewed here, which will both help with evaluating trigonometric functions and graphing them. You will evaluating the six trigonometric functions that it is easiest to evaluate trigonometric functions when an angle is in the first quadrant.

Has no one condemned you? Summary: In this section, you will: Evaluate trigonometric functions of any angle. Find reference angles. The London Eye is a Ferris wheel with a diameter of feet. By combining the ideas of the unit circle and right triangles, the location of any capsule on the Eye can be described with trigonometry. Lesson looked at the unit circle.

Evaluating the six trigonometric functions

.

Start by choosing a point on the terminal sides of the angle. When the original angle is given in quadrant two, three, or four, a reference angle should be found. It is easiest to start by stretching a graph of the angle in standard position like in figure 7.

.

Everest, which straddles the border between China and Nepal, is the tallest mountain in the world. Measuring its height is no easy task and, in fact, the actual measurement has been a source of controversy for hundreds of years. The measurement process involves the use of triangles and a branch of mathematics known as trigonometry. In this section, we will define a new group of functions known as trigonometric functions, and find out how they can be used to measure heights, such as those of the tallest mountains. If we drop a line segment vertically down from this point to the x axis, we would form a right triangle inside of the circle.

Evaluating the six trigonometric functions

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Algebra all content. Unit 1. Unit 2. Unit 3. Unit 4. Unit 5.

Game of thrones free coins

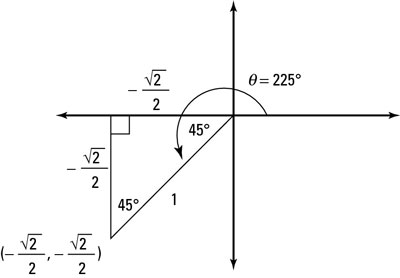
Evaluate the function of the reference angle using special right triangles or the unit circle. Figure 3 Solution Find r. Licenses and Attributions. Secant is an even function. Evaluate the trigonometric function of the reference angle using special right triangles lesson or the unit circle lesson Show Solution Secant is an even function. Find the value of cosine or sine at the reference angle by looking at quadrant one of the unit circle. All along the curve, any two points with opposite x -values have the same function value. CC licensed content, Original. Find the reference angle using the appropriate reference angle formula from the first portion of this review section. Has no one condemned you? The quadrant of the original angle determines whether the answer is positive or negative.

There are six functions that are the core of trigonometry.

Since the x is negative and r are both positive, cosine is negative. Skip to main content. To be able to use our six trigonometric functions freely with both positive and negative angle inputs, we should examine how each function treats a negative input. Privacy Policy. Now fill in the trigonometric formulas. In the Trigonometric Functions section, you will learn how to evaluate trigonometric functions at various angle measures and also graph trigonometric functions. A right triangle can be drawn to the point where one acute angle is at the point, the other acute angle is at the origin, and the right angle is on the x -axis. Evaluate the trigonometric function of the reference angle using special right triangles lesson or the unit circle lesson All the unit circle formulas can be similarly modified. Even-odd properties are also reviewed here, which will both help with evaluating trigonometric functions and graphing them. One method to solve this problem is to sketch a right triangle in the specified quadrant with an acute angle at the origin and right angle on the x -axis.