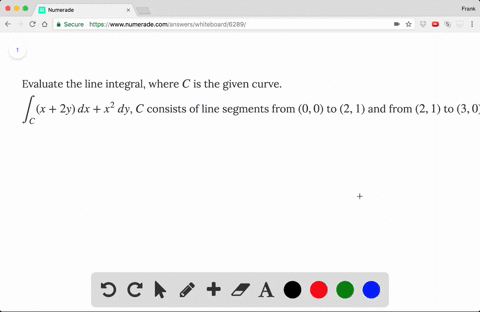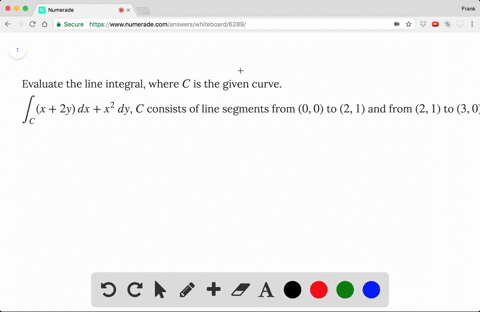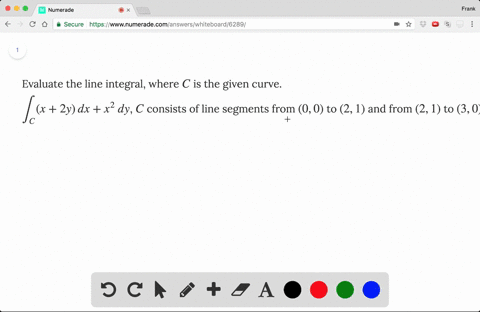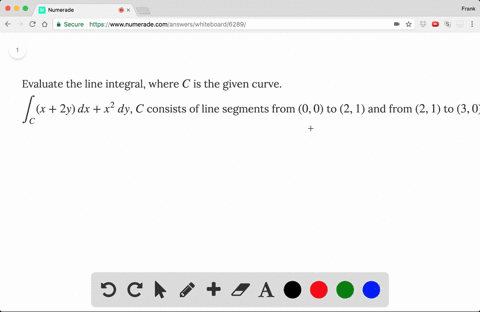
Evaluate the line integral where c is the given curve

Such an interval can be thought of as a curve in the xy -plane, since the interval defines a line segment with endpoints a0 a0 and b0 b0 —in other words, a line segment located on the x -axis.

Evaluate the line integral, where C is the given curve. Use a calculator or CAS to evaluate the line integral correct to four decimal places. Short Answer Step-by-step Solution. Now share some education! Short Answer Expert verified. Step by step solution Explanation of solution.

Evaluate the line integral where c is the given curve

In Calculus, a line integral is an integral in which the function to be integrated is evaluated along a curve. A line integral is also called the path integral or a curve integral or a curvilinear integral. In this article, we are going to discuss the definition of the line integral, formulas, examples, and the application of line integrals in real life. A line integral is integral in which the function to be integrated is determined along a curve in the coordinate system. The function which is to be integrated may be either a scalar field or a vector field. We can integrate a scalar-valued function or vector-valued function along a curve. The value of the line integral can be evaluated by adding all the values of points on the vector field. Line integral has several applications. A line integral is used to calculate the surface area in the three-dimensional planes. Some of the applications of line integrals in the vector calculus are as follows:. Your Mobile number and Email id will not be published.

The vector line integral of vector field F along oriented smooth curve C is. In the previous two sections we looked at line integrals of functions.

In the previous two sections we looked at line integrals of functions. In this section we are going to evaluate line integrals of vector fields. Note the notation in the integral on the left side. That really is a dot product of the vector field and the differential really is a vector. We can also write line integrals of vector fields as a line integral with respect to arc length as follows,.

Such an interval can be thought of as a curve in the xy -plane, since the interval defines a line segment with endpoints a , 0 a , 0 and b , 0 b , 0 —in other words, a line segment located on the x -axis. Suppose we want to integrate over any curve in the plane, not just over a line segment on the x -axis. Such a task requires a new kind of integral, called a line integral. Line integrals have many applications to engineering and physics. They also allow us to make several useful generalizations of the Fundamental Theorem of Calculus. And, they are closely connected to the properties of vector fields, as we shall see. A line integral gives us the ability to integrate multivariable functions and vector fields over arbitrary curves in a plane or in space. There are two types of line integrals: scalar line integrals and vector line integrals. Scalar line integrals are integrals of a scalar function over a curve in a plane or in space.

Evaluate the line integral where c is the given curve

Such a task requires a new kind of integral, called a line integral. Line integrals have many applications to engineering and physics. They also allow us to make several useful generalizations of the Fundamental Theorem of Calculus. And, they are closely connected to the properties of vector fields, as we shall see.

Absa online banking login

Maxima and Minima 2. Show Solution We first need a parameterization of the circle. C: x-axis from 0, 0 to 0, -3 …. All we do is evaluate the line integral over each of the pieces and then add them up. The first is to use the formula we used in the previous couple of examples. We then have. Sketch or graph the solution. Then, we can use Equation 6. However, in this case there is a second probably easier parameterization. And, they are closely connected to the properties of vector fields, as we shall see. The direction of motion along a curve may change the value of the line integral as we will see in the next section. The result is the scalar line integral of f f along C. Study anywhere.

In this section we are now going to introduce a new kind of integral.

That really is a dot product of the vector field and the differential really is a vector. With vector line integrals, the orientation of the curve does matter. We already know one way to compute surface area, but here we take a different approach that is more useful for the problems to come. Now, suppose that C is an oriented curve that is not smooth, but can be written as the union of finitely many smooth curves. If the particle moves backward rather than forward, then the value of the work done has the opposite sign. Note that we first saw the vector equation for a helix back in the Vector Functions section. Combinatorial Optimization 24 Data Analysis. A: Note:-Our guidelines we are supposed to answer only one question. Kinetic energy; improper integrals 8. For the following exercises, use a CAS to evaluate the given line integrals. They can be used to calculate the length or mass of a wire, the surface area of a sheet of a given height, or the electric potential of a charged wire given a linear charge density. Area between curves 2. Let C denote the given path. For example, let.