Equal chords are equidistant from the centre

Well, we see many round objects in daily life like coins, clocks, wheels, bangles, and many more. In this article, we will learn about the equal chords theorem i.

In Mathematics, a chord is the line segment which joins two points on the circumference of a circle. In general, a circle can have infinitely many chords. The distance of the line from a point is defined as the perpendicular distance from a point to a line. If you draw infinite chords to a circle, the longer chord is close to the centre of the circle, than the smaller chord of a circle. In this article, we will discuss the theorem and proof related to the equal chords and their distance from the centre and also its converse theorem in detail. As the perpendicular from the centre of the circle to a chord, bisects the chord, we can write it as.

Equal chords are equidistant from the centre

In the realm of Mathematics, a chord can be described as a line segment that connects two points on a circle's circumference. Interestingly, a circle can have an infinite number of chords. The distance of a line from a point is typically determined by the perpendicular distance from that point to the line. When you draw numerous chords in a circle, you'll notice that the longer chords are closer to the circle's centre than the shorter ones. This article delves into the theorem and proof concerning equal chords and their distance from the centre, as well as its converse theorem. Equal chords in a circle or congruent circles have equal distances from the centre or centres. Since the perpendicular from the centre of the circle to a chord bisects the chord, we can represent this as:. Two intersecting chords of a circle form equal angles with the diameter that passes through their intersection point. Demonstrate that the chords are equal. Last updated on Jul 31, Download as PDF.

Also, read : Circumference of a Circle Congruence of Triangles. Two intersecting chords of a circle form equal angles with the diameter that passes through their intersection point.

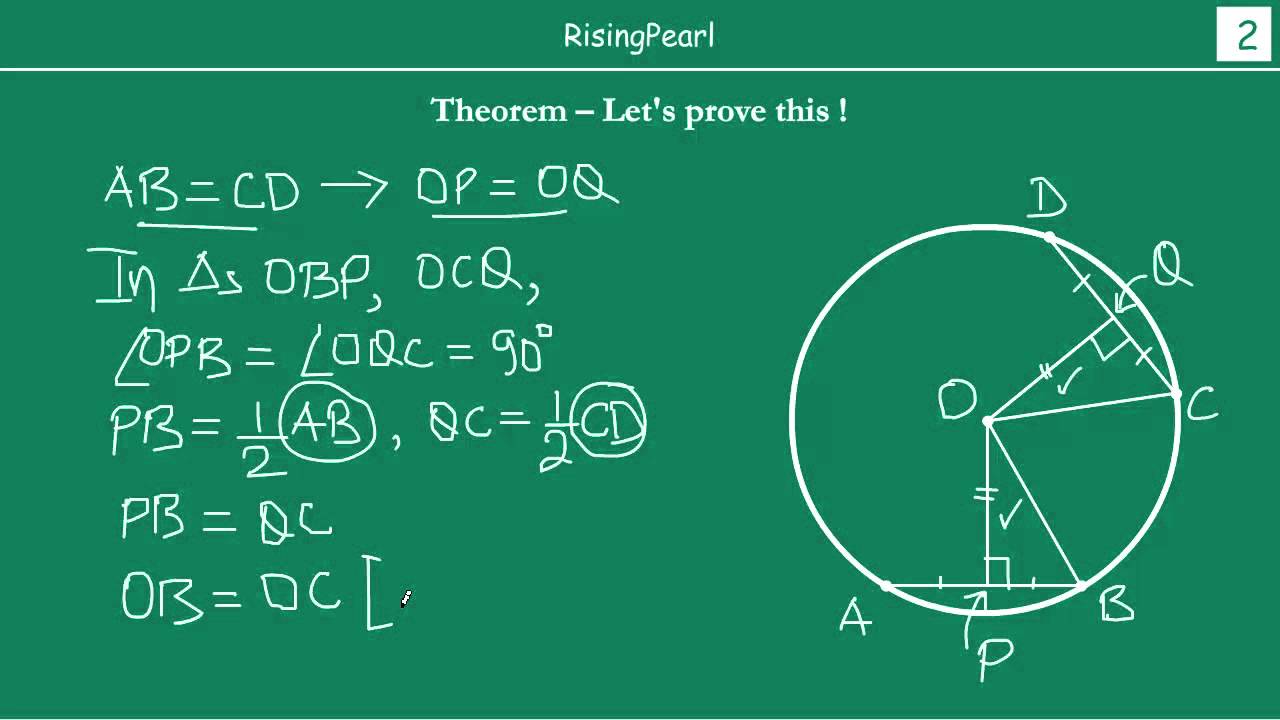
Last updated at March 8, by Teachoo. Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class. Theorem 9. Given : A circle with center at O. AB and CD are two equal chords of circle i.

In the realm of Mathematics, a chord can be described as a line segment that connects two points on a circle's circumference. Interestingly, a circle can have an infinite number of chords. The distance of a line from a point is typically determined by the perpendicular distance from that point to the line. When you draw numerous chords in a circle, you'll notice that the longer chords are closer to the circle's centre than the shorter ones. This article delves into the theorem and proof concerning equal chords and their distance from the centre, as well as its converse theorem. Equal chords in a circle or congruent circles have equal distances from the centre or centres. Since the perpendicular from the centre of the circle to a chord bisects the chord, we can represent this as:.

Equal chords are equidistant from the centre

In Mathematics, a chord is the line segment which joins two points on the circumference of a circle. In general, a circle can have infinitely many chords. The distance of the line from a point is defined as the perpendicular distance from a point to a line. If you draw infinite chords to a circle, the longer chord is close to the centre of the circle, than the smaller chord of a circle. In this article, we will discuss the theorem and proof related to the equal chords and their distance from the centre and also its converse theorem in detail. As the perpendicular from the centre of the circle to a chord, bisects the chord, we can write it as. Two intersecting chords of a circle make equal angles with the diameter that passes through their point of intersection. Prove that the chords are equal.

Youtube adverse childhood experiences

Did not receive OTP? Join Teachoo Black. Maths Classes Teachoo Black. A Perpendicular on the Chord. Download Now. Perpendicular Bisector of the Chord. Book a free demo. To prove: The chords are equal i. Equal chords of a circle make equal angles at the center of a circle. Old search 3. The distance of a line from a point is typically determined by the perpendicular distance from that point to the line.

If XY is 10, what is the length of AB?

Find the length of the common chord. Two concentric circles. Interestingly, a circle can have an infinite number of chords. And point O is the centroid. Maths Classes. Equal Chords and their Distance from the Center Theorem. Determine the length of the common chord if two circles with radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Watch Now. Please login to view more pages. When a line is drawn through the center of a circle that bisects the chord is perpendicular to the chord. A circular road of radius 20m. So, for the chord AB:. Transcript Theorem 9. Displaying ads are our only source of revenue. Teachoo gives you a better experience when you're logged in.