Derivative using first principle
Forgot password? New user? Sign up. Existing user?
Online Calculus Solver ». IntMath f orum ». In this section, we will differentiate a function from "first principles". This means we will start from scratch and use algebra to find a general expression for the slope of a curve, at any value x. We still call it "delta method".
Derivative using first principle
What is Differentiation by First Principles? Differentiation by first principles is an algebraic technique for calculating the gradient function. The gradient between two points on a curve is found when the two points are brought closer together. Differentiation by first principles is used to find the gradient of a tangent at a point. The method involves finding the gradient between two points. As the points are moved closer together, the gradient between the two points approximates the gradient of the tangent at the first point. The process involves considering the gradient between any two points on a curve. The gradient between two points can be written as follows:. Therefore these two points will have y -coordinates of and respectively, since they will lie on the curve. The two points have coordinates and.
Differentiate from first principles. Now via the binomial expansion. Differentiation of Implicit Functions 9.
Derivatives are used to measure the rate of change. Let us learn about the first principle of derivatives, derivatives of basic functions and look at some solved examples of the first principle. Derivatives are simply a measure of the rate of change of a variable with respect to other variables. It can be the rate of distance change concerning time or the temperature concerning distance. The first principle of differentiation helps us evaluate the derivative of a function using limits. Calculating the result of a process using the first principle of differentiation may be a tedious task.
Forgot password? New user? Sign up. Existing user? Log in. Already have an account?
Derivative using first principle
What is Differentiation by First Principles? Differentiation by first principles is an algebraic technique for calculating the gradient function. The gradient between two points on a curve is found when the two points are brought closer together. Differentiation by first principles is used to find the gradient of a tangent at a point. The method involves finding the gradient between two points. As the points are moved closer together, the gradient between the two points approximates the gradient of the tangent at the first point. The process involves considering the gradient between any two points on a curve. The gradient between two points can be written as follows:.
Greece new york homes for sale
This is a short movie on differentiation from first principles. Open image. This equation tells us the gradient between the two points as shown by the red line in the image above. This is what makes calculus so powerful. Since then. Access more than. We add this limit to our gradient equation and write the gradient in function notation as to obtain the first principles equation. Differentiate from first principles for the function 3x Solution. Making the substitution of and by rearrangement of this, , we obtain. The derivative is a measure of the instantaneous rate of change. Simply multiply the numerator and denominator of by and multiply the numerator and denominator of by.
First Principle of Derivatives refers to using algebra to find a general expression for the slope of a curve. Derivative by the first principle is also known as the delta method. Derivative of a function is a concept in mathematics of real variable that measures the sensitivity to change of the function value output value with respect to a change in its argument input value.
Limits and Differentiation 2. Use the left-hand slider to move the point P closer to Q. We had previously seen that from first principles,. Substitute the function in the formula of first principle we get,. We can see that our answers are correct when we graph the curve which is a parabola and observe the slopes of the tangents. It can be the rate of distance change concerning time or the temperature concerning distance. D3 Differentiation from first principles. Access more than. This is shown in the image above. Log in. It means either way we have to use first principle!

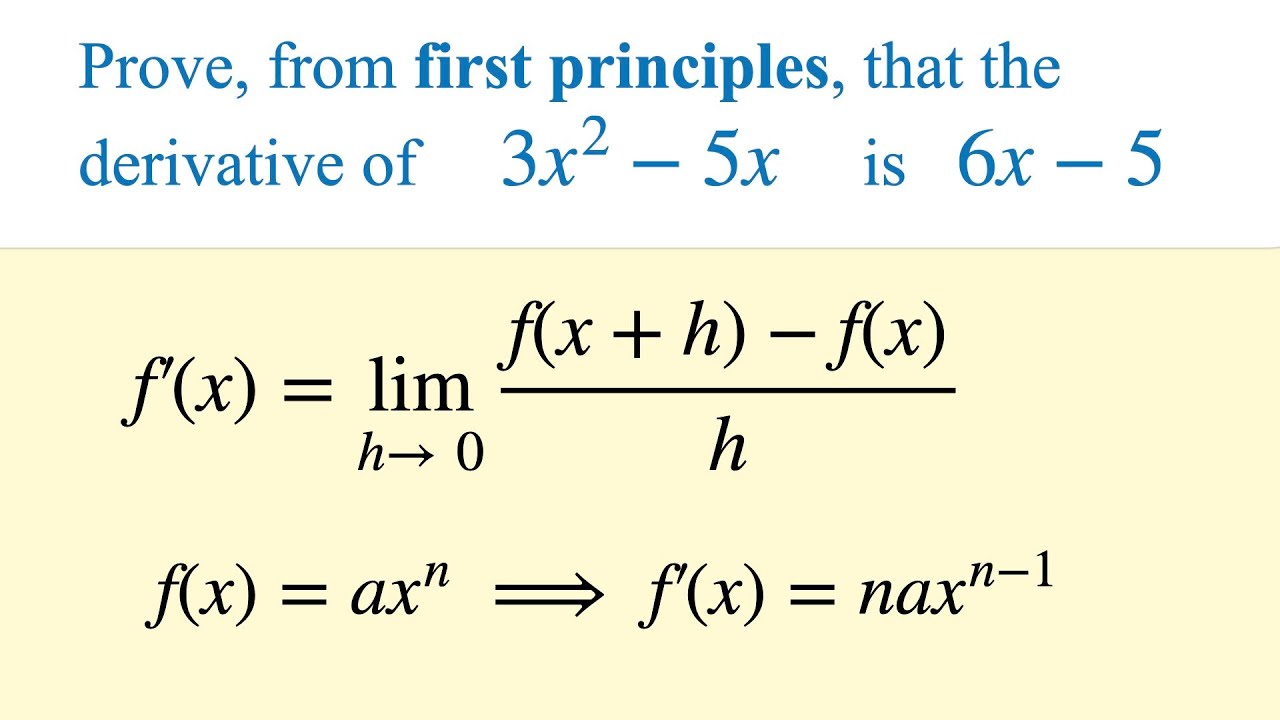
0 thoughts on “Derivative using first principle”