Definition of corresponding angles

Here we will learn about corresponding angles including how to recognise when angles are corresponding and apply this to solve problems.

In this article, we will try to understand what is Corresponding Angles. We will also see the definition, theorem and some examples of Corresponding Angles. Surprisingly, the transversal that meets two parallel lines forms equivalent angles that are congruent. The corresponding angles are not equivalent when the transversal connects two non-parallel lines. When two lines are crossed by another line in plane geometry, corresponding angles are formed. The equivalent angles are the angles formed by matching corners at each junction. In other terms, a comparable angle is one that maintains the same correlative location as another angle in the figure at the same time.

Definition of corresponding angles

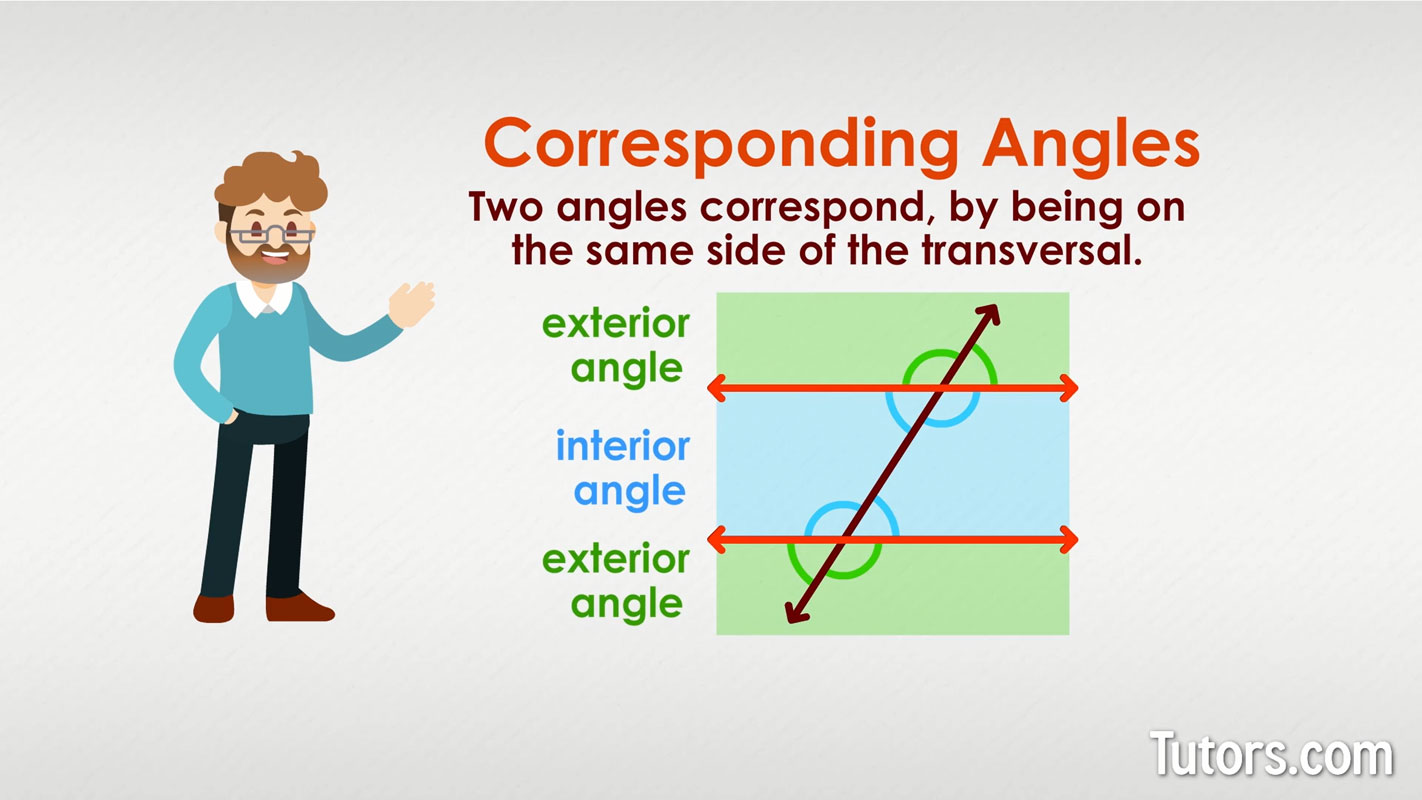
Definition: Corresponding angles are the angles which are formed in matching corners or corresponding corners with the transversal when two parallel lines are intersected by any other line i. For example, in the below-given figure, angle p and angle w are the corresponding angles. Examples of the corresponding angle are any angles which are formed on the opposite side of the transversal. Now, it should be noted that the transversal can intersect either two parallel line or two non-parallel lines. Thus, corresponding angles can be of two types:. In Maths, you must have learned about different types of lines and angles. Here we will discuss only corresponding angles formed by the intersection of two lines by a transversal. The two lines could be parallel or non-parallel. So, let us learn corresponding angles for both the cases. If a line or a transversal crosses any two given parallel lines, then the corresponding angles formed have equal measure.

First, if a transversal intersects two lines so that corresponding angles are congruent, then the lines are parallel. Corresponding angles worksheet.

In geometry, an angle is formed between two rays that share the same endpoint. In our daily life, we see different types of angles formed between the edges of plane surfaces. A pair of angles in a figure can be classified depending upon its position and relationship, such as supplementary angles, alternate angles, vertical angles, and so on. In the following article, we will learn about corresponding angles. Read More Read Less. Two lines on the same plane which never intersect and are equidistant from each other are called parallel lines. A line intersecting two or more lines is known as a transversal.

Corresponding angles are one of the types of angles that are formed when two parallel lines are intersected by the transversal. These are formed in the matching corners or corresponding corners with the transversal. Corresponding angles have important applications in the areas of mathematics and physics. Understanding the corresponding angles is also useful in solving geometry-related problems, such as finding unknown angles or determining congruence between figures, etc. The corresponding angles definition tells us that when two parallel lines are intersected by a third one transversal , the angles that occupy the same relative position at each intersection are known to be corresponding angles to each other. Hence, our corresponding angles definition seems to be justified. We define corresponding angles mathematically as follows: "A pair of angles formed by two parallel lines and a transversal are said to be the corresponding angles if and only if. Corresponding angles are NOT always congruent. We know that each intersection point has 4 angles. Now, each of the four angles in the first intersection region will have another one with the same relative position in the second intersection region.

Definition of corresponding angles

Definition: Corresponding angles are the angles which are formed in matching corners or corresponding corners with the transversal when two parallel lines are intersected by any other line i. For example, in the below-given figure, angle p and angle w are the corresponding angles. Examples of the corresponding angle are any angles which are formed on the opposite side of the transversal. Now, it should be noted that the transversal can intersect either two parallel line or two non-parallel lines. Thus, corresponding angles can be of two types:. In Maths, you must have learned about different types of lines and angles. Here we will discuss only corresponding angles formed by the intersection of two lines by a transversal.

T flip flop minecraft

No corresponding angles can not be considered consecutive interior angles because the consecutive interior angles are the angles that are on the same side of the transversal but inside the two parallel lines. Compare the angles made by the intersection. What is the Angle Rule for Corresponding Angles? Introduction What are Corresponding Angles? Learning checklist. So, the corresponding angles of the given figure are as follows:. JEE Eligibility Criteria Close Privacy Overview This website uses cookies to improve your experience while you navigate through the website. Table of Content. When two lines are crossed by another line in plane geometry, corresponding angles are formed. Still stuck? Read More. English—Polish Polish—English.

A corresponding angle is one that holds the same relative position as another angle somewhere else in the figure.

Corresponding Angles Worksheet. A pair of angles in a figure can be classified depending upon its position and relationship, such as supplementary angles, alternate angles, vertical angles, and so on. Follow us. Find the value of x. The first and second lines are parallel. Our Mission. Example 3: Have you ever come across two parallel streets? Look at the table below to get a better understanding of the different types of corresponding angles. Find out more about our GCSE maths tuition programme. Other lessons in this series include: Angles in parallel lines Alternate angles Co-interior angles. Corresponding angles lie on the same side of the transversal in corresponding positions. In the same, there is no relationship between the interior angles, exterior angles, vertically opposite angles and consecutive angles, in the case of the intersection of two non-parallel lines by a transversal. Download Geometry Worksheets.