Decimal expansion of a rational number is terminating

Let's first define rational numbers before discussing how they are represented when expanded to decimal form. Decimals are what is produced when these numbers are further simplified.

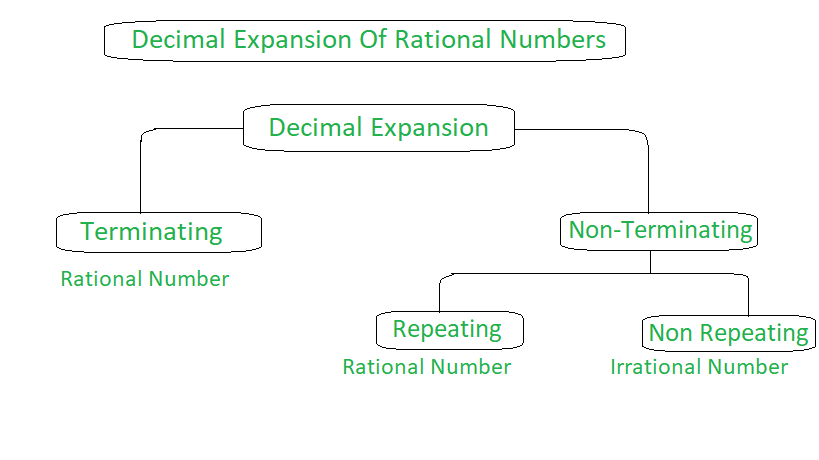
Decimal expansion of rational numbers means when we represent a rational number given in the form of a fraction in the form of a decimal. We use the long division method for this process of conversion. In this math article we will study the decimal expansion of rational numbers. We use the long division method for this process. When we perform the long division method, the quotient obtained after division is the required equivalent value of our rational number in the decimal form. Here as we are not getting the remainder 0 so we terminate the division and consider the quotient got so far.

Decimal expansion of a rational number is terminating

Real numbers are merely the mixture of rational and irrational numerals, in the numeral system. In known, all the arithmetic functions can be achieved on these numerals and they can be expressed in the number line, also. The digits that when represented in decimal format are expressible as non-terminating and non-repeating decimals are understood as irrational numbers. So it is an irrational number. Then, x is a terminating decimal only when q is of the form 2r x 5s for some non-negative integers r and s. Since we understand that by theorem, if a is a prime numeral and if a ranges p 2 , then a divides p, where a is a positive integer. Equation 1 offers 3 as a factor of p and Equation 2 indicates that 3 is a factor of q. This is a paradox to our belief that p and q are co-peaks. Thus, the root of 3 is irrational. Thus, p is a common factor of r and s. But, this contradicts the fact that r and s have no common factor other than 1.

Here, the process of long division goes on. But there are also some rational numbers where the division process does not get terminated as shown in the above example.

A terminating decimal is a decimal in which the digits after the decimal point terminate. This means that the digits after the decimal are finite in number. It is a decimal that has an end-digit. A decimal is a number that consists of a whole number and a fractional part. There are two types of decimals categorized on the basis of the number of digits after the decimal point. If you have two chocolates and you ate half of one of the chocolates, then you are left with 1. This is a terminating decimal since there is only one digit after the decimal point.

Before going into a representation of the decimal expansion of rational numbers, let us understand what rational numbers are. So when these numbers have been simplified further, they result in decimals. Let us learn how to expand such decimals here. Examples: 6 , The real numbers which are recurring or terminating in nature are generally rational numbers. For example, consider the number It can be seen that the decimal part. Also the terminating decimals such as 0.

Decimal expansion of a rational number is terminating

In Mathematics, a real number is a combination of rational numbers and irrational numbers. The rational and irrational numbers can be expressed in their decimal form. The real numbers can be represented using the number line. If the numbers cannot be expressed on the number line, then the numbers are called imaginary numbers. In this article, we are going to learn the real numbers and their decimal expansions in detail. We know that the combination of rational and irrational numbers is called real numbers. Now, we will have a look at the decimal expansion of rational and irrational numbers.

Rae bean vets

How to find the Area of a Regular Polygon? Suggest changes. Saudi Arabia. The digits that when represented in decimal format are expressible as non-terminating and non-repeating decimals are understood as irrational numbers. In terms of decimal, it is a number that ends. The word 'terminate' means to bring to an end. Explore offer now. Then, x is a terminating decimal only when q is of the form 2r x 5s for some non-negative integers r and s. So, this can not be expressed as a rational number. Year 3 Maths. Non-Terminating Decimal Numbers. We use the long division method to convert a rational number to a decimal number.

Terminating decimals are the numbers that have a fixed or a finite number of digits after the decimal point. Decimal numbers are used to represent the partial amount of whole, just like fractions. In this lesson, we will focus on the type of decimal numbers, that is, terminating decimal numbers.

So, it is a terminating decimal number. How to convert a whole number into a decimal? Year 2 Maths. This is because the denominator q has factors other than 2 and 5. But there are also some rational numbers where the division process does not get terminated as shown in the above example. Definition of Terminating Decimal 2. Year 1 Maths. Hence the division never gets terminated and the quotient goes upto infinity. A decimal is a number that consists of a whole number and a fractional part. Contribute your expertise and make a difference in the GeeksforGeeks portal. Hence, p is irrational. Explore math program.