Cos x sin 2x
Please ensure that your password is at least 8 characters and contains each of the following:. Enter a problem Trigonometry Examples Popular Problems.
Please ensure that your password is at least 8 characters and contains each of the following:. Enter a problem Trigonometry Examples Popular Problems. Use the double - angle identity to transform to. Add to both sides of the equation. Simplify the left side.
Cos x sin 2x
.
Divide each term in by and simplify. List the new angles. Multiply by by adding the exponents.
.
Solve Practice Play. Game Central. Greatest Common Factor. Least Common Multiple. Order of Operations. Mixed Fractions. Prime Factorization. Solve for a Variable. Evaluate Fractions. Linear Equations.
Cos x sin 2x
Cos2x is one of the important trigonometric identities used in trigonometry to find the value of the cosine trigonometric function for double angles. It is also called a double angle identity of the cosine function. The identity of cos2x helps in representing the cosine of a compound angle 2x in terms of sine and cosine trigonometric functions, in terms of cosine function only, in terms of sine function only, and in terms of tangent function only. Cos2x identity can be derived using different trigonometric identities. Let us understand the cos2x formula in terms of different trigonometric functions and its derivation in detail in the following sections. Cos2x is an important trigonometric function that is used to find the value of the cosine function for the compound angle 2x. We can express cos2x in terms of different trigonometric functions and each of its formulas is used to simplify complex trigonometric expressions and solve integration problems. Cos2x is a double angle trigonometric function that determines the value of cos when the angle x is doubled. Cos2x is an important identity in trigonometry which can be expressed in different ways. It can be expressed in terms of different trigonometric functions such as sine , cosine, and tangent.
Walmart couch set
Divide each term in by. Trigonometry Examples Popular Problems. Step 6. Simplify the expression to find the second solution. The absolute value is the distance between a number and zero. The complete solution is the result of both the positive and negative portions of the solution. The cosine function is positive in the first and fourth quadrants. Simplify the denominator. Next, add this reference angle to to find the solution in the third quadrant. Simplify the right side. To find the second solution , subtract the reference angle from to find the solution in the second quadrant. Rewrite in terms of sines and cosines. Use the power rule to combine exponents. Add to to find the positive angle. Move to the left of.
In trigonometry, sin, cos, and tan are the basic trigonometric ratios used to study the relationship between the angles and sides of a triangle especially of a right-angled triangle. Pythagoras worked on the relationship between the sides of a right triangle through the Pythagorean theorem while Hipparcus worked on establishing the relationship between the sides and angles of a right triangle using the concepts of trigonometry.
Combine and. Find the period of. If any individual factor on the left side of the equation is equal to , the entire expression will be equal to. Subtract from both sides of the equation. Multiply by. This website uses cookies to ensure you get the best experience on our website. The period of the function is so values will repeat every radians in both directions. Add to both sides of the equation. Divide each term in by. Multiply by. Apply the distributive property. Replace with in the formula for period. Divide each term in by and simplify. Take the inverse sine of both sides of the equation to extract from inside the sine.

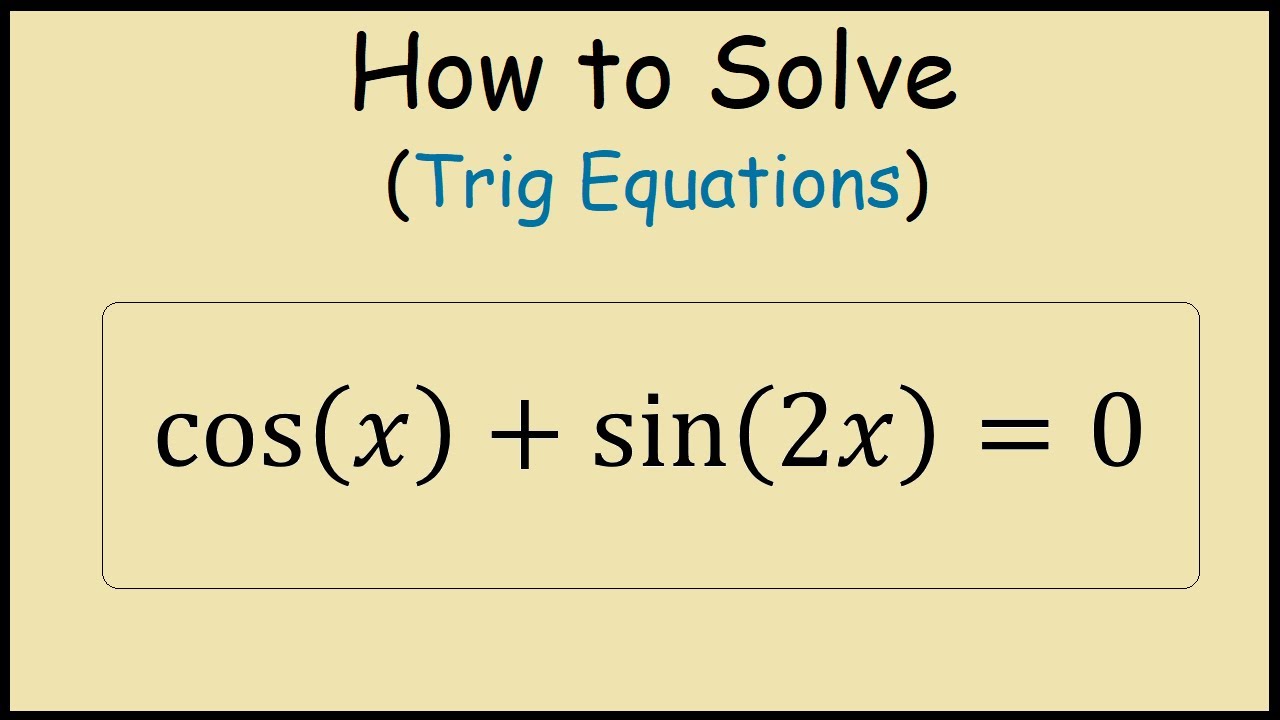
0 thoughts on “Cos x sin 2x”