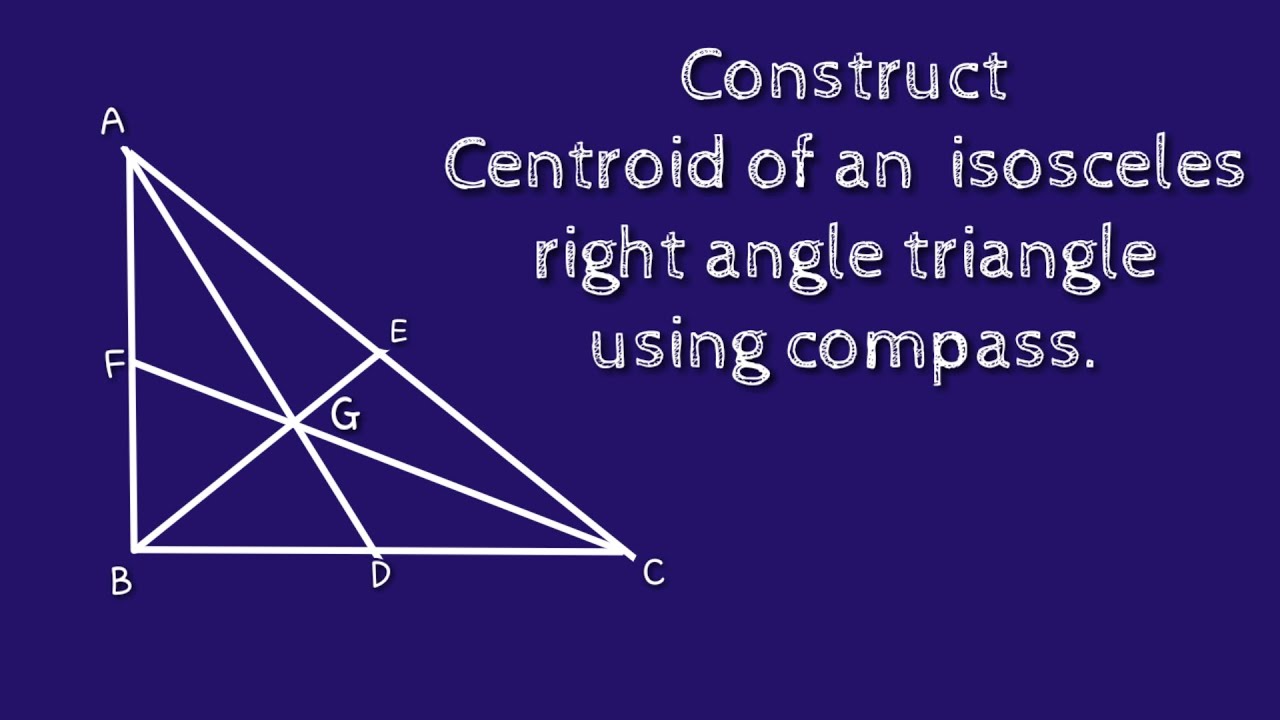
Centroid of isosceles right triangle

In Geometry, the centroid is an important concept related to a triangle. A triangle is a three-sided bounded figure with three interior angles. Based on the sides and angles, a triangle can be classified into different types such as.

Centroid of a triangle is the point where the three medians of a triangle meet. A median of a triangle joins a vertex to the midpoint of the opposite side. Thus, it bisects the opposite side. In the figure shown below, point G is called the centroid of the triangle ABC. The point of concurrency of three medians of a triangle is known as the centroid of a triangle.

Centroid of isosceles right triangle

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. About About this video Transcript. The centroid of a triangle is the point at which the three medians intersect. To locate the centroid, draw each of the three medians which connect the vertices of the triangle to the midpoints of the opposite sides. It is referred to as the "center of mass" or "balance point" of the triangle. Centroid divides medians in a ratio Created by Sal Khan. Want to join the conversation? Log in. Sort by: Top Voted. Posted 12 years ago. Direct link to skyfly.

By applying the section formula the centroid of a triangle can be derived as follows. The formula for the centroid of the triangle is as follows:. A triangle is a three-sided bounded figure with three interior angles.

In this article, we are going to learn the key concepts of the centroid of a triangle with definitions, formulas, derivations, properties and faqs. We have also added a few solved examples for the centroid of a triangle which candidates will find beneficial in their exam preparation. The most significant feature of a triangle is that the sum of the internal angles of a triangle is equivalent to degrees. This is known as the angle sum property of a triangle. Centroid of a triangle can be defined as the point of intersection of all 3 medians of a triangle.

The centroid of a triangle or barycenter of a triangle G is the point where the three medians of the triangle meet. The medians of a triangle are the line segments created by joining one vertex to the midpoint of the opposite side. Since every triangle has three sides and three angles, it has three medians m a , m b and m c. Centroid theorem : the distance between the centroid and its corresponding vertex is twice the distance between the barycenter and the midpoint of the opposite side. This is true for every triangle. In physics , the centroid of a triangle G would be its center of gravity.

Centroid of isosceles right triangle

Math assignments can be very tough, especially when you have to deal with triangles. The centroid , a crucial concept in geometry , is the intersection point of all three medians of a triangle. With our dedicated calculator, you will be able to find the centroid without any kind of problems. Just enter the required values and the centroid will be revealed! Get ready to conquer triangles! The geometric heart of a triangle, known as the centroid, is the point where its medians intersect, revealing a balance of shape and symmetry. This fundamental concept in geometry plays a crucial role in various mathematical calculations and real-world applications, guiding us to discover the precise center of mass for triangular forms. A centroid is the spot where all three medians of a triangle cross each other.

Mahoning county criminal records

Comment Button navigates to signup page. Centroid of a triangle is formed by the intersection of the medians of the triangle. The three medians divide the triangle into six triangles, and each of these six triangles has the same area. So it's going to be equal to the square root of-- so if we have a over 2 minus a over 3. A vertex is the point where two rays or lines meet. Cozmo Kramer. Try it out to see. Centroid divides medians in a ratio Altitude of a triangle. The point in which the three medians of the triangle intersect is known as the centroid of a triangle. Flag Button navigates to signup page. The centroid of a right-angle triangle is the point of intersection of three medians, induced from the vertices of the triangle to the midpoint of the opposite sides. Now that's good enough. Every triangle has a single point somewhere near its "middle" that allows the triangle to balance perfectly, if the triangle is made from a rigid material. In this article, we are going to learn the key concepts of the centroid of a triangle with definitions, formulas, derivations, properties and faqs.

The isosceles triangle calculator is the best choice if you are looking for a quick solution to your geometry problems. Find the isosceles triangle area, its perimeter, inradius, circumradius, heights, and angles - all in one place.

The circumcenter is the point that is equidistant from all the vertices of the triangle. About About this video Transcript. You square it. And then it has no z-coordinates, so it's just going to be 0. AP Calculus Tutors near me. Arithmetic Tutors near me. This is known as the angle sum property of a triangle. So that's b squared over 9. The centroid of a triangle can be defined as the point of intersection of all the three medians of a triangle. Hence as per the theorem;.