Center 5 6 tangent to the x axis

Q: Determine the center and radius of each circle in general form.

First, we start with the standard circle equation. Then, we can plug in the center coordinates we're given to this standard equation. So what's missing from our standard equation is the r. How do we find that? When you graph, you have that point at 1, -3 and then you should have a vertical line that crosses the x-axis at 6,0. Since we know the center of our circle is 1, -3 and we know that at any tangent line to a circle, the distance from the center to that tangent line intersecting the circle is the radius.

Center 5 6 tangent to the x axis

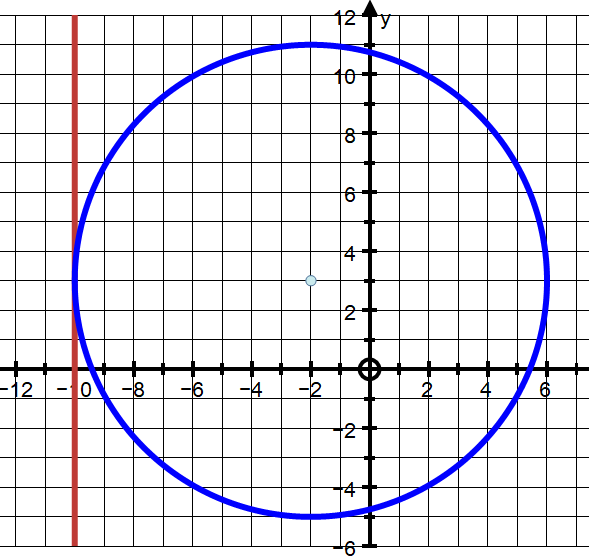
I am completely lost with this one. How do I get the y-coordinate? When a circle is tangent to the x axis it's either completely above it or completely below it. Here we know there's a point in the first quadrant, so the circle is above the x axis. The radius at the tangent point 1,0 must be perpendicular to the x axis, i. So if the radius is length r then the center coordinates must be 1,r. Find the equation of a circle passing through 5,6 and tangent to the x-axis at 1,0? Dean R. Apr 21, Explanation: When a circle is tangent to the x axis it's either completely above it or completely below it. Related questions How do I determine the molecular shape of a molecule? What is the lewis structure for co2? What is the lewis structure for hcn? How is vsepr used to classify molecules? What are the units used for the ideal gas law?

Q: Calculate the equation of the circle that passes through the point 0, -3whose radius is V5 and…. Q:

.

This calculator can find the center and radius of a circle given its equation in standard or general form. Also, it can find equation of a circle given its center and radius. The calculator will generate a step by step explanations and circle graph. Welcome to MathPortal. I designed this website and wrote all the calculators, lessons, and formulas. If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]. Math Calculators, Lessons and Formulas It is time to solve your math problem. Calculators :: Analytic Geometry :: Circle equation calculator.

Center 5 6 tangent to the x axis

In the standard coordinate plane, what is the radius and the center of the circle? When finding the center and radius of circle , the center is and the radius is. Notice that they are not negative even though in the equation they have negative signs in front. This becomes important when dealing with real numbers. Also, notice the square of. Our circle, has the same principles applied as the above principle, therefore is our center. Notice how the numbers signs have been switched. This is the case for all circles due to the negative in the base equation above. To find the radius of a circle, you must take the number the equation is equal to and square root it. This is due to the square of mentioned above.

M betper 23

Ask a question for free Get a free answer to a quick problem. Elementary Geometry For College Students, 7e. SLO 11 A:. Equation of…. A: See the details solution below. A: We have to find the center and radius of given circle. Find the equation of the circle that has a center at 3, 3 and is tangent to the y- axis? So if the radius is length r then the center coordinates must be 1,r. Find the center and radius of the circle defined by the equation given below. Which of the following points…. Then draw its graph.

.

SLO 11 A:. Since we know the center of our circle is 1, -3 and we know that at any tangent line to a circle, the distance from the center to that tangent line intersecting the circle is the radius. Q: III. Similar questions. Q: Write the standard equation of a circle with the center at -1, -4 that passes through the point… A:. Q: Find the equation of the circle in standard form satisfying the given conditions: C 7,4 externally…. Find the center and radius of the circle defined by the equation given below. What are the units used for the ideal gas law? Kindly repost other question as…. Q: Find equation of the circle in general form that satisfies the given condition. Author: Swokowski.